PROBLEM LINK:
Author: Praveen Dhinwa
Tester: Utkarsh Lath
Editorialist: Balajiganapathi Senthilnathan
Russian Translator: Sergey Kulik
Mandarian Translator: Gedi Zheng
DIFFICULTY:
Easy
PREREQUISITES:
Basic Graph
PROBLEM:
For a birthday party, n persons can be invited. The i-th person gives Rs. r_i (can be negative too, in case, you have to give that person |r_i| rupees) as gift but requires that f_i th person must also be present. What is the maximum amount of money that can be earned from the gifts.
SHORT EXPLANATION
Build a graph with n nodes. There is an edge from f_i to i for all i. Note that this graph only consists of a number of components each having a simple cycle with possibly a few simple paths going out from it. For each component, we sum the values of all gifts in the cycle and do a dfs away from the cycle. For each path from the cycle, if the sum of values is positive, we add the value to the total value of the component. If the total value of the component is positive then we can add them to our answer otherwise we won’t invite anyone from this component.
EXPLANATION:
Consider a graph with n nodes corresponding to the n persons. We add a directed edge from f_i to i. What this means is that, if there is an edge from a to b, then we have to invite person a if we want to invite person b. Also, if we have invited a person x, then we can potentially invite all those nodes which have an incoming edge from x. Note that in this graph, each node has exactly one incoming edge. An example graph is shown below for input
11
2 0
3 0
2 0
3 0
6 0
8 0
6 0
7 0
6 0
5 0
5 0
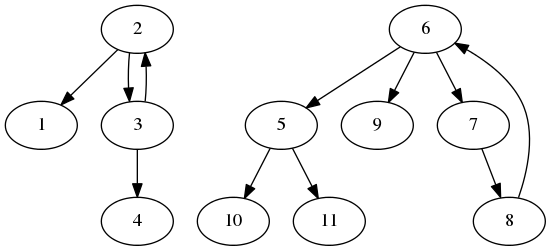
If we draw such a graph for a few examples, we will find a pattern in the graph: the graph is made up of a number of (weakly connected) components each of which has exactly one simple cycle and possibly few paths going out from the cycle. Let us formally prove this observation. Suppose there is a component which does not have any cycle, then there must be a node which does not have any incoming edge - a contradiction.
To proceed we observe that inviting a person in one component does not affect our choices in another component. Thus, we can calculate the maximum value we can get for each of the components one by one and sum them up.
Let us see how we can solve for a particular component. First note that if we are to invite anyone from this component then we have to invite everyone from the cycle. So, we sum the values of all nodes in the cycle. We can now consider this cycle as a single node having this value. So, now we have to determine the maximum value we can get.
Here is the important observation: if for a node x, we have invited some people who require node x to be invited directly or indirectly, then the sum of the values of these people have to be non negative. Because otherwise we can exclude these people from the party and have a better total amount. This gives us an idea for the algorithm: for each node x, we solve recursively for each of its children (i.e nodes to which there is an outgoing edge from x). We invite a children only if we can get a positive value after inviting it. Finally, we sum up all such values from the children and add the node’s own value to this sum. If this total value is positive then we can return it else it will be better to not invite x or anyone who depends on x, so we return 0.
For each component, we call the above procedure starting from the cycle node and add the answer we got for all the components to get the total gift amount.
Implementation Notes
Now, how can we find the cycle corresponding to a single connected component? First note that, we just have to find a single vertex lying in the cycle, then we will go from i to f_i and so on and thus we will find the entire cycle.
So, for finding a single vertex lying in the cycle, let us construct a graph G of n nodes where edges are from f_i to i. Now, pick any vertex in the component and keep taking the only outward edge in the graph. Finally, in the end, you will reach one vertex which surely lies in the cycle.
Time Complexity:
O(n)