PROBLEM LINK:
Author: Praveen Dhinwa
Tester: Istvan Nagy
Editorialist: Miguel Oliveira
DIFFICULTY:
Simple
PREREQUISITES:
Graph Theory
PROBLEM:
Given a positive integer N up to 50, find if the following algorithm computes the longest shortest path in any connected undirected graph with N vertices. If it doesn’t, output any graph in which this algorithm doesn’t work correctly.
Algorithm (start_vertex):
find out the set of vertices S having maximum value of
shortest distance from start_vertex.
ans = 0;
for each vertex v in S
temp = 0;
for each vertex u in graph G:
temp = max(temp, shortest distance between u and v).
ans = max(ans, temp);
return ans;
EXPLANATION:
The given algorithm works if the given graph was a tree (explanation). However, as the problem statement suggests, it does not always work in a general graph.
This problem is unusual. Instead of finding an algorithm to solve a problem, we need to find out why the given algorithm is incorrect. So, pen and paper are best to tackle this challenge!
Without loss of generality, I will assume for simplicity that there is only one vertex S furthest away from start_vertex. For the algorithm to be flawed, S can not be one the two end-points of the longest shortest path. Also, S must be closer to all vertices than the length of the longest shortest path.
The simplest way to do this is to use a longest shortest path of length 4, put S at distance 3 away from start_vertex and all other vertices at distances 1 or 2 from start_vertex.
Suppose the longest shortest path is a path like 1 - 2 - 3 - 4 - 5 (length 4). To have start_vertex at distance up to 2 to all of them, adding edges (start_vertex, 2), and (start_vertex, 4) is sufficient.
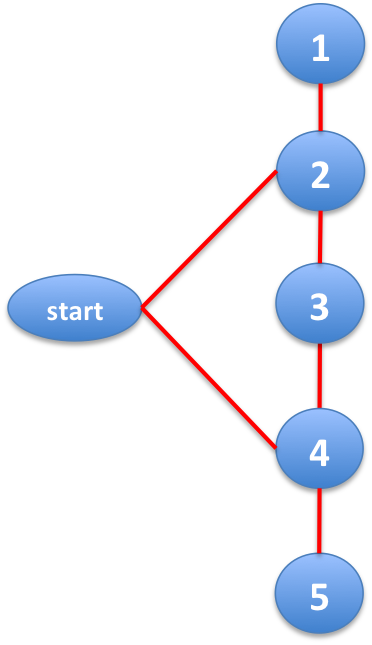
Now, we want to have S at distance 3 from start_vertex and distance at most 3 from the others so that we can’t find a path of length 4 from S. So we connect S to vertex 3.

Finally, we can connect all the other vertices to either vertices 2 or 4. This way, all of them are at distance 2 from start_vertex and distance 3 from S. Hence, the algorithm will only find paths of length up to 3.
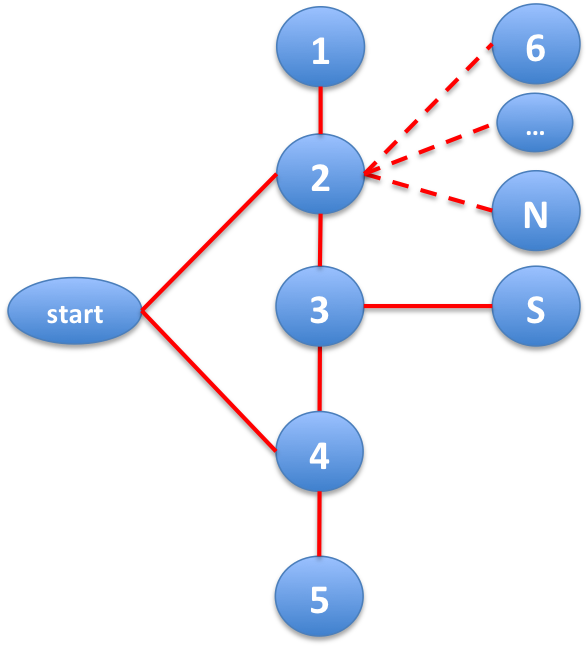
To be able to use this construction, we need at least 7 vertices. So, there is always a counter-example if N \ge 7. We can check by brute force that it’s impossible to do this if N \leq 6.
For each input, we only need N edges, so the time complexity of this approach is O(N) per test case.