I tried to solve This problem and solved it with complexity on O(n^2). I tried to find pattern to solve this question, but couldn’t find any.
Can anyone see any pattern in this problem, help me out.
I tried to solve This problem and solved it with complexity on O(n^2). I tried to find pattern to solve this question, but couldn’t find any.
Can anyone see any pattern in this problem, help me out.
Yes, it can be done in O(1). Since, answer must be less than K, therefore maximum possible answer we can get is K-1.
If you convert K into binary representation you can see that if K is odd you can always get K-1 using (K-1)&K but if K is even then by above observation K-2 is always possible but we need to check if K-1 is possible or not. We can do this by taking A as K-1 and B as the number which gives K-1 on applying AND operator with A and that would be K|(K-1). So we can take B as K|(K-1) but we have to ensure that B<=N. If B<=N then answer is K-1 else K-2.
The constant time solution is given in the link you provided. You just had to switch tabs. The below constant time solution is given in the ‘Discussions’ tab and another constant time solution is given in the ‘Editorial’ tab.
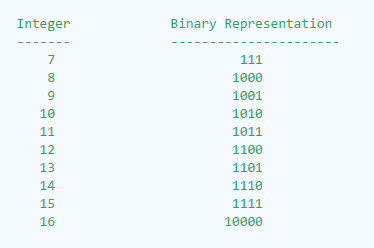
Observation : We need result < k, hence, the best possible result is k-1.
Now, if k is odd, then k-1 is even. By looking at binary pattern above, it can be easily observed that k-1 can be achieved using (k-1) & k since only last bit is different.
Conclusion 1 : if k is odd, answer is (k-1)
The other possibility is k is even. Here, the binary pattern shows that k-1 may or may not be possible to reach. But, since k-1 is odd, by “Conclusion 1”, we know that k-2 is reachable.
Conclusion 2 : if k is even, (k-2) is always achievable
So, we know that required answer is either k-1 or k-2, because at least one of the two is achievable and all other values will be worse than them. Now, we need to check if k-1 can be achieved with even k.
Let’s assume that its possible to get k-1 as result of bitwise & between two integers. Since, “bitwise &” between two integers is always less than or equal to operand integers, both integers need to be >= k-1. To select the minimum possible integers, first integer = k-1. Now, the other integer can only be >=k. Also, “bitwise &” need to return back k-1. Hence, smallest integer satisfying these properties = (k-1) with least significant “0-bit” modified to “1” = (k-1)|k. Since, this value can be larger than k, we should make sure that it is a value that we can access i.e. (k-1)|k <= n.
Conclusion 3 : if k is even and (k-1)|k <= n, answer is (k-1)
If the above condition isn’t true, k-1 cannot be the result. It is also known that if k-1 cannot be achieved, k-2 can definitely be achieved. This implies that answer can only be k-1 or k-2. Moreover, if k is odd, k|(k-1) = k since only last bit is different. It’s given that k<=n, therefore, (k-1)|k <= n.
Conclusion 4 : if k is odd, (k-1)|k <= n
Combining the above conclusions, we can easily sum up the result.
Result : if (k-1)|k <= n, then k-1, else k-2
Code:

Your approach is really nice, but how you figured that out. K|K-1 will be the number which will give K-1 on applying & operator.
@arpit728 thanks, as B is greater than A(i.e., K-1), therefore B>=K and it must give K-1 on applying & operator with A, therefore B must have those bits set to 1 as that of K-1 and we also want the number to be greater than K-1 such that B remains less than N, hence the next number greater than K-1 we can have would be K|K-1.