Does unsigned matter? ( YES )

help
,
1

Hello friends ,

In the SQRDSUB problem from long challenge , I got wrong answer when I used long long int and got partial marks in the same code when I used unsigned long long int

Long long int , Wa , Absolute value :

https://www.codechef.com/viewsolution/31861811

Unsigned long long int , partial AC ( Absolute value not needed ) :

https://www.codechef.com/viewsolution/31655065

%4 , long long int , Wa , Absolute value :

https://www.codechef.com/viewsolution/31861832

%4 , unsigned long long int , partial AC ( Absolute value not needed ) :

https://www.codechef.com/viewsolution/31861896

Pls let me know why this is happening
Thanks
:slight_smile:

1 Like
2

it only matters because when you are taking input in an array , you areinserting a negative integer in an array and later changing it to its absolute value. unsigned will be required here because if we go in order you are taking “A negative integer first as input” it doesn’t matter if you later change a[i] to abs(a[i])

1 Like
3

@mshaheer2003 , thanks for pointing out
I have added new links and in all of them where absolute value is required i am doing but still getting wa
Pls let me know why
Thanks :slight_smile:

4

Why ?

5 
for(ll i = 0; i < n; i++){

    ll product = a[i];

    if(a[i]%2 == 1 || a[i]%4 == 0 || a[i] == 0) count++;

    for(ll j = i+1; j < n; j++){
        product *= a[j];
        if(product%2 == 1 || product%4 == 0 || product == 0) count++;
    }
}

I believe the above should be the problem.

Remember, A[i] ≤ 10^9 and N ≤ 10^3 (for the first subtask)

The product of the whole array will be (10^9)^{(10^3)}, which, obviously, is beyond the limits of C++ (unsigned) long long int.

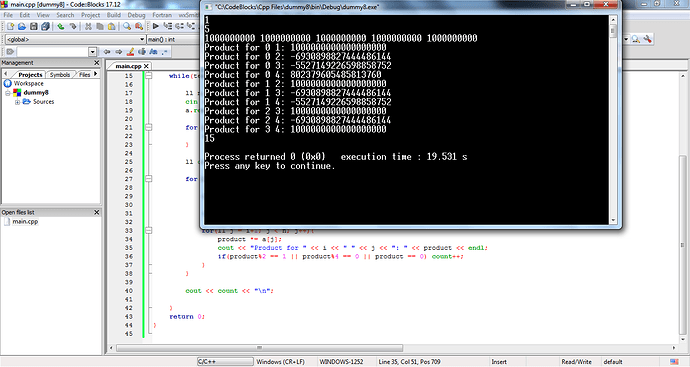
I took a small example, an array of length 5, and printed the product for each (i, j).

image
image1366Ă—728 112 KB

Somehow (for most of the testcases), the overflowed product retains the same modulo as the actual product.

So I created a random testcase generator.

This is a testcase for which your code outputs 124715, but the answer according to my code, another code, and your code with unsigned long long is 124755.

I’m not sure what the issue is, but playing with overflow is a bad idea.

2 Likes
6

@crap_the_coder
That’s because, overflow in unsigned long long int is equivalent to mod 2^{64}, and he’s only checking mod 4. Since 4 divides 2^{64}, it still works.
Even signed long long int does mod 2^{64}, but anything above 2^{63}\ mod \ 2^{64}, becomes negative, so product%2==1 won’t hold. You also have to check product%2==-1.
https://www.codechef.com/viewsolution/31864303

2 Likes
7

Ohhh, wow! Great observation! I forgot that in C++, -1 % 2 = -1 unlike Python

1 Like