I tried to solve this problem by((h*w)*(h*w))as total possible tilings but in editorial total is
2^(h+w). Can anyone explain why this is so?
Link of the problem: C. Tiles
3 Likes
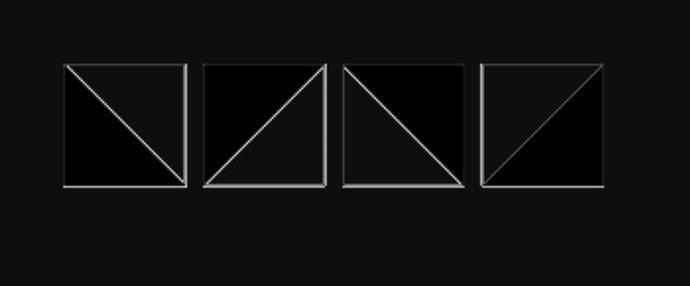
Consider this picture
Let us label them as A,B,C,D.
As you can observe from the picture, there are only 2 choices to tile a square to its right for every pair. That is, A or B will be followed only by A or B. Both these choice is valid. Similarly, C and D will only be followed by C or D.
If we continue like this, we will observe that that, there are exactly
2^(h+1) ways to tile the top most row.Now similarly, if we tile the row below the top most low, there are exactly 2 choices for the left most square. For each of these two choices, there is exactly one choice for the square to its right, and so on.
So observing this, we get that the entire row is determined by the row above and the left-most tile in that row. So for an wxh grid, there are 2^(h+w) possible tilings.
Hope this clears your doubt

2 Likes
Thanks for explaining it clearly. Just one more doubt, why it is 2^ (h+1) and not 2^(h).
If you just consider the top left square of the 1st row, you will see that we have 4 choices for this square (i.e. one below it and one adjacent). Now for any of these 4 choices, there are 2 ways to tile the square right of this square. So for every row, we have h+1 choice and for every choice, we have 2 ways, So total 2^(h+1) ways
1 Like