PROBLEM LINK:
Author: Sunita Sen
Tester: Arnab Chanda
Editorialist: Sunita Sen
DIFFICULTY:
EASY - MEDIUM
PREREQUISITES:
GRAPH-BFS/DFS,Dijkstra
PROBLEM:
Given a graph and two nodes S and K find the number of shortest simple paths from S to K.
EXPLANATION:
We will be using DFS to solve this problem.
Let us look at DFS code:
DFS(G, s):
mark s as visited
for all neighbours w of s in Graph G:
if w is not visited:
DFS(G, w)
But hey, visiting nodes is not enough we must add weight of path:
DFS-withweight(G, sum, s):
mark s as visited
for all neighbours w of s in Graph G:
if w is not visited:
sum = sum + weight[s][w] // weight[s][w] weight of path s->w
DFS(G, sum, w)
However, this method will fail when two separate paths will converge at a node, and both will lead to a minimum value path.
Like this one:
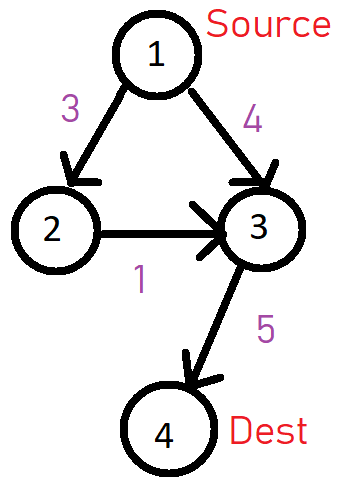
Say we follow the path 1->3->4 then we will be marking node 3 as visited, then 2->3->4 will become invalid.
So we can do this:
DFS-withweight(G, sum, s):
for all neighbours w of s in Graph G:
if w is not visited:
mark s as visited
sum = sum + weight[s][w] // weight[s][w] weight of path s->w
DFS(G, sum, w)
sum = sum - weight[s][w]
mark s as not visited
Lastly, we need to store the count of shortest simple paths. If the path sum from S to K is already equal to minimum sum, then we will increment our count value, and if path sum is less than minimum sum, then, we will set the minimum sum and count value will be equal to 1.
DFS-withweight(G, sum, s):
if s is equal to k:
if sum < minimum sum:
minimum sum = sum
count = 1
else if sum = minimum sum:
count = count + 1
return
for all neighbours w of s in Graph G:
if w is not visited:
mark s as visited
sum = sum + weight[s][w] // weight[s][w] weight of path s->w
DFS(G, sum, w)
sum = sum - weight[s][w]
mark s as not visited
Bonus: Solving using dijkstra
We can also solve this problem using dijkstra’s algorithm.
Number of shortest simple path till K can be reached in two ways:
Let a parent of K is some node A.
- If the path sum between S to K via A is less than the already calculated path sum of K: The number of shortest paths from S to K will be equal to number of shortest paths from S to A.
- If the path sum between S to K via A is equal to the already calculated path sum of K: The number of shortest paths from S to K will be equal to number of shortest paths from S to K + number of shortest paths from S to A.
Here, we will keep calculating the number of shortest paths for each node as we calculate the minimum distance from source to a vertex in dijkstra’s algorithm.
Refer to: Soham Chakrabarti’s solution
SOLUTIONS:
Setter's Solution
#include<bits/stdc++.h>
using namespace std;
#define rep(i,n) for(ll i=0;i<(n);i++)
#define FOR(i,a,b) for(ll i=(a);i<(b);i++)
#define dfor(i,a,b) for(ll i=(a);i>=(b);i--)
#define mem(u, vis) memset(u, vis, sizeof(u))
#define ll long long
#define ull unsigned long long
#define MOD 1000000007
#define MAX 1e9
#define pb push_back
#define F first
#define S second
const ll INF = 1e9;
vector<pair<ll,ll>> v[1000];
bool visited[2000];
ll minsum = INF,amt=0;
void dfs(ll k,ll sum,ll target){
if(k == target){
if(sum<minsum){
minsum = sum;
amt = 1;
}
else if(sum==minsum){
amt++;
}
return;
}
for(auto i: v[k]){
if(!visited[i.F]){
visited[i.F] = true;
dfs(i.F,sum+i.S,target);
visited[i.F] = false;
}
}
}
int main() {
ll t=1;
cin>>t;
while(t--){
minsum = INF;
amt = 0;
ll n,m;
cin>>n>>m;
rep(i,m){
ll a,b,c;
cin>>a>>b>>c;
v[a].push_back(make_pair(b,c));
}
ll k,s;
cin>>s>>k;
dfs(s,0,k);
cout<<amt<<endl;
rep(i,n){
v[i].clear();
}
mem(visited,false);
}
}