Editorial - ICM2003

1

PROBLEM LINK:

Practice
Div-1+2 Contest

Author: Bhagya Kamal Jain
Tester: Jatin Yadav
Editorialist: Bhagya Kamal Jain

DIFFICULTY:

MEDIUM

PREREQUISITES:

Binary/Ternary Search, Calculus

PROBLEM:

You are given a function f(x)=(x2+b∗x+c)/sin(x) find its minimum value in the interval 0<x<π/2

QUICK EXPLANATION:

Binary Search over x in the range to find the root of it’s derivative. Or Apply ternary search to find the minimum value directly.

EXPLANATION:

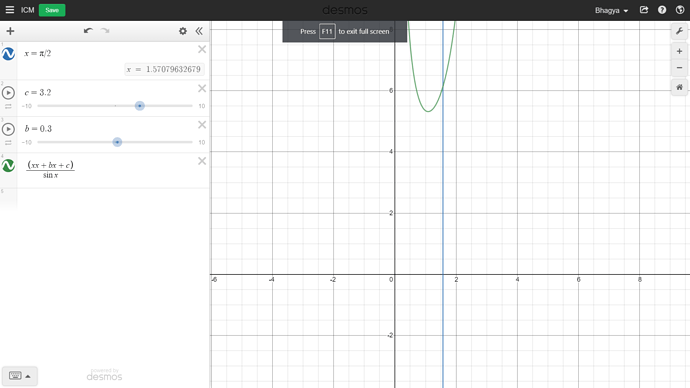
You may look at the graph to confirm that f(x) is convex in the interval. Though it is possible to prove it mathematically.

Screenshot%20(90)
Screenshot%20(90)1920×1080 86.1 KB

Observe that that the function f(x) is convex in the given interval.

Ie. Its derivative is strictly increasing in the given interval.

Find the root of f’(x) by applying Binary Search. Minimum value of the function occurs at this value.

Then output the value of f(x) for the given x.

ALTERNATE EXPLANATION:

Apply ternary search,read about it here.
Refer to author’s solution for the same.

SOLUTIONS:

Setter's Solution

CodeChef: Practical coding for everyone

Editorialist's Solution

CodeChef: Practical coding for everyone

2

@bhj2001 why are you running the loop from i=0 to i=50 ? . If I do while(r-l > \epsilon) in ternary search, where \epsilon is 10e-9, why am I getting TLE ? In this submission.

3

Sorry for the super late reply.
TLDR : both are same.
Basically in each couple iteration of the loop you increase the precision of the answer by a digit, so I choose number of iterations according to what the time TL allows.

1 Like
4

Also, the solution you wrote TLEed, which will not be an issue if you fix the number of iterations.

1 Like