PROBLEM LINK
Contest link
Setter: Kunal Jain
Tester: Announcement
DIFFICULTY
Medium
PREREQUISITES
Observation, basic coordinate geometry
PROBLEM
Given a set of N circles, the code needs to remove the least number of circles such that the resulting set does not contain a circle that entirely encloses another circle. Find the bug in the code.
BUGGY CODE
pastebin
EXPLANATION
There is no bug in the code of the problem. The code takes a greedy approach to the problem, where if one circle is entire enclosed by another circle, it removes the out circle.
This greedy strategy fails in the case when there are multiple circles enclosing the same small circles, that dont enclose each other. Something of the form of this:
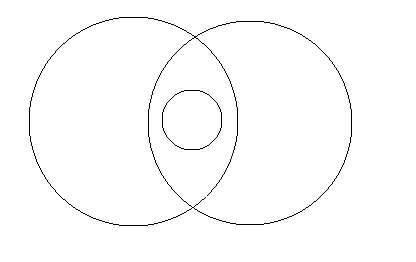
Such a case can be created by:
3
100 5 0
100 -5 0
1 0 0
If greedy fails then how can we solve this problem?
I’m afraid this is a vertex cover problem, which is in NP-hard class, so any non-greedy exact solution has to use some form of trial an error. To reduce this problem to graph – imagine each circle as a vertex, and if circle A encloses circle B there is an edge from A to B. Here, we need to find the minimum subset of circles that are incident to all of the edges, so that removing them causes no edges to exist. Then the only restriction we have – if there is an edge from A to B, from B to C then there is an edge from A to C. However, since the graph is directed, but we are essentially searching an undirected vertex cover, I don’t think this restriction simplifies the problem
How about this?, someone shared this approach on codeforces blog,
Let’s create a directed graph where an edge goes from node A to node B when circle A is totally enclosed by circle B. It is easy to see that this graph will be a DAG Now, the problem is to find the longest anti-chain in this DAG. This can be done using Dilworth’s theorem.
