PROBLEM LINK:
Practice
Contest: Division 1
Contest: Division 2
Contest: Division 3
Contest: Division 4
Author: Soumyadeep Pal
Testers: Jeevan Jyot Singh, Hriday
Editorialist: Nishank Suresh
DIFFICULTY:
1288
PREREQUISITES:
None
PROBLEM:
Given an array A of length N, decide whether it can be partitioned into two arrays B and C that have an equal number of distinct elements.
EXPLANATION:
The answer is “No” if and only if N is odd and all the elements of A are distinct.
Proof
Let N be odd and all the elements of A be distinct. Then, no matter how the partition is done, B and C will have different sizes (and their number of distinct elements equals their size, so equality is impossible).
Now we have to prove that a suitable division always exists in the other case.
- Suppose A has an even number of distinct elements — for convenience, let’s call them 1, 2, 3, \ldots, 2K. Then, put all occurrences of 1, 2, \ldots, K into B and all occurrences of K+1, K+2, \ldots, 2K into C. B and C now have K distinct elements each, as required.
- Suppose A has an odd number of distinct elements — let them be 1, 2, \ldots, 2K+1. Note that, in particular, 2K+1 \lt N, so some element occurs greater than once — let one such element be x.
Now, create B and C as in the even case by assigning all elements other than x. Finally, place one copy of x in B and the others in C. B and C both have K+1 distinct elements now.
This completes the proof.
Checking the above condition can easily be done with a frequency table in \mathcal{O}(N) since the array elements are \leq N.
TIME COMPLEXITY
\mathcal{O}(N) per test case.
CODE:
Setter's code (C++)
#include<bits/stdc++.h>
using namespace std;
int main() {
int tt;
cin >> tt;
while (tt--) {
int n;
cin >> n;
vector<int> a(n);
for (int i = 1; i <= n; i++) {
int x;
cin >> x;
a[x - 1]++;
}
if (n % 2 == 1 && *max_element(a.begin(), a.end()) == 1) {
cout << "NO\n";
} else {
cout << "YES\n";
}
}
return 0;
}
Editorialist's code (Python)
for _ in range(int(input())):
n = int(input())
a = list(map(int, input().split()))
distinct = len(set(a))
print('yes' if (distinct%2 == 0 or distinct < n) else 'no')
3 Likes
- if distinct elements are even then no worries they will divide
- if odd only one element with frequency > 1 is needed to satisfy
void solve(){
int n;
cin>>n;
vi arr(n);
repi(0,n-1) cin>>arr[i];
map<int,int> m;
repi(0,n-1) m[arr[i]]++;
if((int)m.size()==1){
auto it = (*m.begin()).first;
if(m[it] <= 1){
cout<<"NO\n";
return;
}
}else{
int size = m.size();
if(size%2 != 0){
bool check = false;
for(auto x : m){
if(x.second > 1){
check = true;
break;
}
}
if(!check){
cout<<"NO\n";
return;
}
}
}
cout<<"YES\n";
}
What if we take n=4
And array elements 1 1 1 3 ??
1 Like
one array will contain 3 the other will contain 111
Thanks now I got it
I thinks that we should divide the array into B and C with equal no of elements
1 Like
This is my code but it passes only one tc does any one have any edge cases where it fails?
edit: so basically if even it will some how form so even == yes
and if odd then also will form eg 2 3 1 1 1 = 1 2 and 3 1 and will form only exception if all the numbers are unique
#include
#include
#include
#include
#include
using namespace std;
#define ll long long int
int main(){
ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0); //this is fast I/O (inputput output) use header file <cstdio>
ll t;cin>>t;
while(t--){
ll n; cin>>n;
ll a[n];
map<ll,ll>freq;
for(int i=0; i<n; i++){
cin>>a[i];
freq[a[i]]++;
}
if(n%2!=0)
cout<<"NO"<<endl;
else{
ll unique = 0, odd=0;
for(auto it:freq){
if(it.second==1)
unique++;
else if(it.second%2!=0)
odd++;
}
if((unique+odd)%2==0)
cout<<"YES"<<endl;
else
cout<<"NO"<<endl;
}
}
return 0;
}
What you’re saying is correct, but that isn’t what your code is doing.
if (n%2 == 0) cout << "NO" << endl; is obviously wrong, even on the example you provided.
Try to simplify your code and implement exactly the things you said, and you will get AC:
- If all the numbers are distinct and the array size is odd, the answer is no
- Otherwise the answer is yes
1 Like
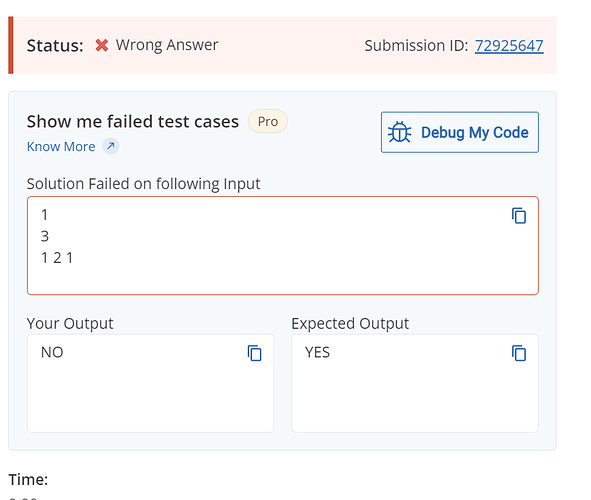
plz explain how 1 2 1 can be divide into two parts such that each part has same n.o of distinct elements…
/* package codechef; // don't place package name! */
import java.util.*;
import java.lang.*;
import java.io.*;
/* Name of the class has to be "Main" only if the class is public. */
class Codechef
{
public static void main (String[] args) throws java.lang.Exception
{
// your code goes here
Scanner sc = new Scanner(System.in);
int tc = sc.nextInt();
while(tc-- > 0){
int n = sc.nextInt();
int []arr = new int[n];
Set<Integer> set = new HashSet<>();
int count = 1;
boolean flag = false;
HashMap<Integer, Integer> map = new HashMap<>();
for(int i=0; i<n; i++){
arr[i] = sc.nextInt();
set.add(arr[i]);
if(map.containsKey(arr[i])){
map.put(arr[i], map.get(arr[i] + 1));
if(!flag){
count++;
flag = true;
}
} else{
map.put(arr[i], 1);
}
}
// if there are Even Distinct Elements then they will divide
if(set.size()%2 == 0){
System.out.println("YES");
}else{
// In Case of Odd Distinct Elements one Elements with freq > 1 is required
if(count > 1){
System.out.println("YES");
}else{
System.out.println("NO");
}
}
}
}
}
oh I thought order has to stay same…ok thanks anyway
1 Like