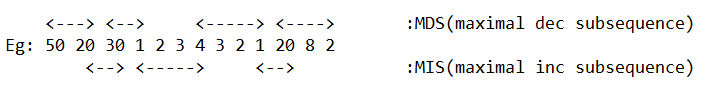Problem Link:
Author: sahi1422
Tester enchom
Editorialist: Sabre
Prerequisites: STL
Difficulty: Easy
Effective Question: Check if the number of maximal inc/dec contiguous subsequences in a given range(L,R) are equal or not, for Q queries.
L=1,R=13
MIS:3
MDS:4
Verdict: NO
Explanation:
We fix flags(store positions) 0 and 1 to denote the behaviour of an arbitrary subsequence:
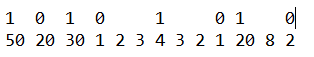
Going from 0 to 1 implies the subsequence is increasing and vice versa. A single loop running over the length is sufficient for this task.
A few observations follow:
- This sequence will always be alternating in nature: 010101… or 1010101… and hence any subsequence of these flags will be so too.
- Not counting the last flag, # of 0’s will give # of MIS and # of 1’s will give the # of MDS in range L=1 and R=N. This is true for any arbitrary subsequence too(with any L or R).
Now we take Q queries each consisting of a “L” and a “R”.
Now each L and R will be between some positions of our preset flags. They may even coincide onto these flags(4 cases). For instance this is one possible case:
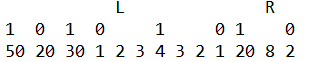
Now we find the nearest left flag wrt L(is 0 for above) and nearest right flag wrt R(is 0 for above). There maybe 4 possible cases:(00,01,10,11) We treat the cases (00,11) as similiar and (01,10) as similiar.
- Case: 00/11
Only odd lengths will be allowed.
Eg: 010/101 length=3;
Eg: 01010/10101 length=5;
and so on. So here we note that the #0’s=#1’s if we exclude the last flag. From observation 2 the #MIS=#MDS always for this case.
- Case: 01/10
Only even lengths will be allowed.
01,0101,010101…,10,1010,101010,…
and so on. So here we note that the #0’s!=#1’s if we exclude the last flag. From observation 2 the #MIS and #MDS will never be equal for this case.
So it all comes down to finding the nearest left flag wrt L and nearest right flag wrt R !
There can be many efficient ways to do this but one way that comes to mind is to use a multiset because of its very efficient insert,find,erase operations.
It will be a simple 5 step process(Assuming L and R are not present initially in the set):
Complexity:
O(N) for fixing the flags. O(logN+logN+logN) for each query, total Q queries so: O(3QlogN).
Overall complexity: O(N+3QlogN) which is O(N+Q).
Solution Link:
Sabre
Comments:
Enjoyed writing my first unofficial editorial ![]()
Thought of writing taster instead of tester(if you know, you know xD) ![]()