PROBLEM LINK:
Author: Fang Lixing
Tester: Hanlin Ren
Editorialist: Hanlin Ren
DIFFICULTY:
EASY
PREREQUISITES:
Math, Graph Theory
PROBLEM:
Given an undirected graph G=(V,E), partition the vertex set V into as few as possible (disjoint) subsets, such that the induced subgraph of each subset contains an even number of edges.
QUICK EXPLANATION:
- If the graph itself has an even number of edges, we can “divide” it into one set;
- Otherwise, |E| must be odd. If the degree of some vertex v is odd, then we partition V into \{v\} and V-\{v\};
- Otherwise we pick any edge (u,v)\in E, and partition V into \{u\}, \{v\} and V-\{u,v\}.
EXPLANATION:
It’s easy to see that if the graph itself contains an even number of edges, then we can “divide” it into one set and K=1. The number of edges belonging to this set is even.
If the graph contains an odd number of edges, then there are two cases:
Case 1: If there is a vertex v whose degree \deg(v) is odd, then we can partition the vertices into K=2 sets: the first set is \{v\}, and the second set is V-\{v\}. The number of edges in the first set is 0, and the number of edges in the second set is |E|-\deg(v). Since both |E| and \deg(v) is odd, this solution is valid.
Case 2: Suppose the degree of every vertex is even. It’s impossible to partition the vertices into 2 sets, such that every set has an even number of edges.
Proof
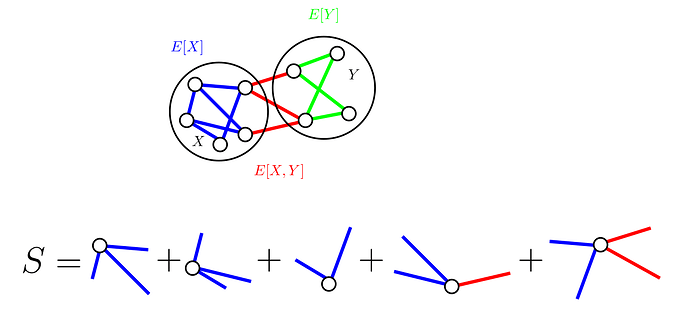
Assume, for the sake of contradiction, that V=X\cup Y is such a partition.
We denote E[X] as the set of edges in the induced subgraph of X, and E[Y] as the set of edges in the induced subgraph of Y. We also let E[X,Y] be the set of edges between X and Y. Let’s count the sum of degrees of vertices in X, and denote it by S, i.e. S=\sum_{x\in X}\deg(x). Since every vertex has even degree, S should be an even number. However
- For each edge in E[X], it’s counted twice in S;
- For each edge in E[Y], it doesn’t affect S at all;
- For each edge in E[X,Y], it’s counted once in S.
Therefore the parity of S should be equal to the parity of |E[X,Y]|. Since there are an odd number of edges in G, but an even number of edges in both E[X] and E[Y], we know that |E[X,Y]| is odd, a contradiction. QED.
Can we do it in three sets? The answer is YES! We pick any edge e=(u,v) that’s in E, and partition V into three sets \{u\},\{v\} and V-\{u,v\}.
We still need to prove that V-\{u,v\} contains an even number of edges. The edges not in the induced subgraph of V-\{u,v\} are either the edges incident to u, or the edges incident to v. Since both \deg(u) and \deg(v) are even, it seems that there are an even number of edges not in V-\{u,v\}. However, we counted the edge (u,v) twice! If we subtract this edge, we know that the number of edges not in V-\{u,v\} is odd. And since G has an odd number of edges, V-\{u,v\} contains an even number of edges, and we’re done.
Time complexity is O(N+M).
ALTERNATE EXPLANATION:
Please feel free to share your approaches ![]()
SOLUTIONS:
Setter's Solution
#include <cstdio>
#include <algorithm>
int read() {
int w = 1, q = 0, ch = ' ';
for (; ch < '0' || ch > '9'; ch = getchar()) if (ch == '-') w = -1;
for (; ch >= '0' && ch <= '9'; ch = getchar()) q = q * 10 + ch - 48;
return q * w;
}
const int N = 100010;
int n, m, deg[N], u, v;
void Main() {
// answer <= 3
n = read();
m = read();
for (int i = 1; i <= n; i++) {
deg[i] = 0;
}
for (int i = 1; i <= m; i++) {
u = read();
v = read();
deg[u] ^= 1;
deg[v] ^= 1;
} // read, and calculate the parity of degree
if (!(m & 1)) {
putchar('1'), putchar('\n');
for (int i = 1; i <= n; i++) {
putchar('1'), putchar(' ');
}
putchar('\n');
return;
} // the whole graph is okay, answer = 1
for (int i = 1; i <= n; i++) {
if (deg[i]) {
putchar('2'), putchar('\n');
for (int j = 1; j <= n; j++) {
if (j != i) {
putchar('1'), putchar(' ');
} else {
putchar('2'), putchar(' ');
}
}
putchar('\n');
return;
}
} // if a vertex got odd degree, divide it, answer = 2
putchar('3'), putchar('\n');
for (int i = 1; i <= n; i++) {
if (i == u) {
putchar('2'), putchar(' ');
} else if (i == v) {
putchar('3'), putchar(' ');
} else {
putchar('1'), putchar(' ');
}
}
putchar('\n'); // divide the end point of any edge, answer = 3
}
int main() {
int T = read();
while (T--) {
Main();
}
return 0;
}
Tester's Solution
#include <bits/stdc++.h>
using namespace std;
void gi(int &x) {char ch = getchar(); x = 0; while (ch < '0' || ch > '9') ch = getchar(); while (ch >= '0' && ch <= '9') x = x * 10 + ch - 48, ch = getchar();}
void pi(int x) {if (x > 9) pi(x / 10); putchar(x % 10 + 48);}
int u[102020], v[102020], deg[102020];
void doit() {
int n, m, i, j;
gi(n); gi(m);
for (i = 1; i <= n; i++) deg[i] = 0;
for (i = 1; i <= m; i++) {
gi(u[i]); gi(v[i]);
deg[u[i]]++; deg[v[i]]++;
}
if (~m & 1) {
pi(1); putchar('\n');
for (i = 1; i <= n; i++) pi(1), putchar(' ');
} else {
for (i = 1; i <= n; i++) if (deg[i] & 1) break;
if (i <= n) {
pi(2); putchar('\n');
for (j = 1; j <= n; j++) {
if (j == i) pi(2); else pi(1);
putchar(' ');
}
} else {
pi(3); putchar('\n');
for (j = 1; j <= n; j++) {
if (j == u[1]) pi(2);
else if (j == v[1]) pi(3);
else pi(1);
putchar(' ');
}
}
}
putchar('\n');
}
int main() {int t; gi(t); while (t--) doit(); return 0;}