PROBLEM LINK:
Practice
Contest: Division 1
Contest: Division 2
Setter: tasmeemreza
Tester: Raja Vardhan Reddy
Editorialist: Taranpreet Singh
DIFFICULTY:
Medium
PREREQUISITES:
Dynamic Programming, Barricade DP problem
PROBLEM:
Given an array A of length N, select subset S of exactly K distinct indices such that C = \sum_{i \in S} \sum_{j \in S} f(i, j) is minimized where f(i, j) denotes the maximum of A_l, A_{l+1} \ldots A_r. Find this minimum value of C.
QUICK EXPLANATION
- Convert given array into a binary tree, by taking maximum element as the root and recursively building tree in the left and right segments.
- Let’s compute the minimum cost of choosing K indices in the subtree of u in a bottom-up manner. For node u, if we have selected x indices in the left subtree and y indices in the right subtree, then x*y times, node u shall be on the path. Since node u shall have the largest value in the subtree of u, it shall be added x*y times. We can similarly handle the case when node u is also chosen.
EXPLANATION
Let us suppose we are given an array [4,5,1,3,2] and K = 3
Let’s convert it into a binary tree as follows.
Find the maximum element and its position. In our case, maximum element is 5 and its position p = 2. The left child is built recursively on array [4] and right child is built on [1,3,2]
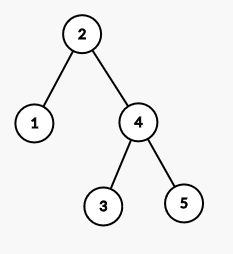
The above tree has the property that for f(i, j), the maximum element shall appear at the LCA of node i and node j in the above tree.
Now, let us discuss a seemingly slow solution to solve this.
Let’s for each node, compute the minimum cost of choosing x indices (nodes) in the subtree of u. We shall compute it in a bottom-up manner, so assume we have already calculated it for all immediate children of u.
Also, let C_{u, x} denote the minimum C for selecting x nodes in subtree of u
If node u is a leaf, then we can select either node u or not select it. So we get C_{u, 0} = 0 and C_{u, 1} = A_u
Otherwise, let’s calculate C_{u, x} for each x.
Also, Suppose u has only one child, labeled ch1.
For a fixed x, we have two cases, selecting all x nodes in the child’s subtree or choosing node u and choosing x-1 nodes in the child’s subtree. In the first case, the minimum cost is given by C_{ch1, x}. In the second case, the cost is given as C_{ch1, x-1} + x*A_u, as there are x-1 intervals started in subtree of ch1 which end at u and one interval f(u, u) which contributes A_u, giving C_{ch1, x-1} + x*A_u.
Hence, C_{u, x} = min(C_{ch1, x}, C_{ch1, x-1} + x*A_u)
Lastly, node u may have two children.
In this case, we may select y nodes in subtree of left child ch1, and x-y nodes in subtree of the right child ch2 and may or may not choose to select node u.
This gives C_{u, x} = min_{y = 1}^x(C_{ch1, y}+C_{ch2, x-y} + y*(x-y)*A_u) if node u is not chosen. y*(x-y)*A_u comes from the fact that y nodes in left subtree shall each pair with x-y nodes in right child’s subtree exactly once, giving y*(x-y) paths crossing node u, each path having cost A_u
If node u is chosen, we get C_{u, x} = min_{y =1}^{x-1} (C_{ch1, y}+C_{ch2, x-y-1} + (y+1)*(x-y)*A_u)
(y+1)*(x-y) comes from the number of paths crossing node u, y*(x-y-1) pairs of type (v, w) where v is in left subtree and w is in right subtree, y pairs of type (v, u), x-y-1 pairs of type (u, w) and one pair (u, u). All of them have cost A_u. Hence, we get A_u*(y*(x-y-1)+y+(x-y-1)+1) = A_u*(y+1)*(x-y)
Using the above transitions, we can calculate the C_{u, x} for all nodes u and all values of x.
The above solution is currently O(N^3) since for each node, we have to iterate over N^2 pairs (y, x-y). But we are doing a lot of useless work. Let S_u denote the number of nodes in subtree of node u. Then, there’s no way to select z > S_u nodes in subtree of node u.
Hence, we should iterate only over those pairs (y, x-y) such that 0 \leq y \leq S_{ch1} and 0 \leq x-y \leq S_{ch2} holds. Now the same solution has time complexity O(N^2)
Proof of time complexity
Let us consider all pairs of nodes (u, v). We can see that only time this pair of nodes is considered in different subtrees of the same node, is when processing the node LCA(u, v). Since there are N^2 pairs and each pair is considered exactly once, the overall time complexity is O(N^2) per test case.
Problems to try
PAINTREE and STTT are worth a try. Also, reading problem Barricades from the book Looking for a Challenge would be helpful.
Lastly, the above solution doesn’t depend on the value of K at all. Does your solution depend? Share in comments.
TIME COMPLEXITY
The time complexity is O(N^2) per test case.
SOLUTIONS:
Setter's Solution
#include "bits/stdc++.h"
using namespace std;
int a[5005];
vector <int> g[5005];
long long dp[5005][5005];
long long fn[10][5005];
int sub[5005];
const long long inf = 26000000000000000LL;
int N, K;
int make_tree(int l, int r) {
if(l == r) {
return l;
}
int opt = l;
for(int i = l; i <= r; i++) {
if(a[opt] < a[i]) {
opt = i;
}
}
if(l < opt) {
g[opt].push_back(make_tree(l, opt - 1));
}
if(opt < r) {
g[opt].push_back(make_tree(opt + 1, r));
}
return opt;
}
void dfs(int x) {
sub[x] = 1;
for(auto i : g[x]) {
dfs(i);
sub[x] += sub[i];
}
int c = g[x].size();
for(int i = 0; i <= c; i++) {
for(int j = 0; j <= K; j++) {
fn[i][j] = inf;
}
}
int size = 1;
fn[0][0] = 0;
fn[0][1] = a[x];
for(int i = 1; i <= c; i++) {
int y = g[x][i - 1];
for(int j = 0; j <= size; j++) {
for(int k = 0; k <= sub[y]; k++) {
if(j + k > K) continue;
fn[i][j + k] = min(fn[i][j + k], fn[i - 1][j] + dp[y][k] + 1LL * j * k * a[x]);
}
}
size += sub[y];
}
for(int i = 0; i <= sub[x]; i++) {
dp[x][i] = fn[c][i];
}
}
int main(int argc, char const *argv[])
{
int test;
scanf("%d", &test);
for(int cs = 1; cs <= test; cs++) {
int n, k;
cin >> n >> k;
N = n; K = k;
for(int i = 1; i <= n; i++) g[i].clear();
for(int i = 1; i <= n; i++) {
cin >> a[i];
}
int root = make_tree(1, n);
dfs(root);
cout << dp[root][k] << endl;
}
return 0;
}
Tester's Solution
//raja1999
//#pragma comment(linker, "/stack:200000000")
//#pragma GCC optimize("Ofast")
//#pragma GCC target("sse,sse2,sse3,ssse3,sse4,avx,avx2")
#include <bits/stdc++.h>
#include <vector>
#include <set>
#include <map>
#include <string>
#include <cstdio>
#include <cstdlib>
#include <climits>
#include <utility>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <iomanip>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
//setbase - cout << setbase (16)a; cout << 100 << endl; Prints 64
//setfill - cout << setfill ('x') << setw (5); cout << 77 <<endl;prints xxx77
//setprecision - cout << setprecision (14) << f << endl; Prints x.xxxx
//cout.precision(x) cout<<fixed<<val; // prints x digits after decimal in val
using namespace std;
using namespace __gnu_pbds;
#define f(i,a,b) for(i=a;i<b;i++)
#define rep(i,n) f(i,0,n)
#define fd(i,a,b) for(i=a;i>=b;i--)
#define pb push_back
#define mp make_pair
#define vi vector< int >
#define vl vector< ll >
#define ss second
#define ff first
#define ll long long
#define pii pair< int,int >
#define pll pair< ll,ll >
#define sz(a) a.size()
#define inf (1000*1000*1000+5)
#define all(a) a.begin(),a.end()
#define tri pair<int,pii>
#define vii vector<pii>
#define vll vector<pll>
#define viii vector<tri>
#define mod (1000*1000*1000+7)
#define pqueue priority_queue< int >
#define pdqueue priority_queue< int,vi ,greater< int > >
#define int ll
typedef tree<
int,
null_type,
less<int>,
rb_tree_tag,
tree_order_statistics_node_update>
ordered_set;
//std::ios::sync_with_stdio(false);
int node=0,iinf=inf;
int left_child[5005],right_child[5005],val[5005],a[5005],dp[5005][5005],siz[5005];
int buildtree(int i,int j){
if(i==j){
val[node]=a[i];
left_child[node]=-1;
right_child[node]=-1;
return node;
}
int maxx=0,k,id,cur_node;
f(k,i,j+1){
maxx=max(maxx,a[k]);
}
f(k,i,j+1){
if(a[k]==maxx){
id=k;
break;
}
}
cur_node=node;
if(id==i){
node++;
left_child[cur_node]=buildtree(i+1,j);
right_child[cur_node]=-1;
}
else if(id==j){
node++;
right_child[cur_node]=buildtree(i,j-1);
left_child[cur_node]=-1;
}
else{
node++;
left_child[cur_node]=buildtree(i,id-1);
node++;
right_child[cur_node]=buildtree(id+1,j);
}
val[cur_node]=maxx;
return cur_node;
}
int compute(int u){
siz[u]=1;
int i,j;
if(left_child[u]==-1 && right_child[u]==-1){
dp[u][0]=0;
dp[u][1]=val[u];
return 0;
}
if(left_child[u]!=-1){
compute(left_child[u]);
siz[u]+=siz[left_child[u]];
}
if(right_child[u]!=-1){
compute(right_child[u]);
siz[u]+=siz[right_child[u]];
}
if(right_child[u]==-1){
rep(i,siz[u]+1){
dp[u][i]=iinf;
}
rep(i,siz[left_child[u]]+1){
dp[u][i]=min(dp[u][i],dp[left_child[u]][i]);
dp[u][i+1]=min(dp[u][i+1],dp[left_child[u]][i]+val[u]*(i+1));
}
return 0;
}
if(left_child[u]==-1){
rep(i,siz[u]+1){
dp[u][i]=iinf;
}
rep(i,siz[right_child[u]]+1){
dp[u][i]=min(dp[u][i],dp[right_child[u]][i]);
dp[u][i+1]=min(dp[u][i+1],dp[right_child[u]][i]+val[u]*(i+1));
}
return 0;
}
rep(i,siz[u]+1){
dp[u][i]=iinf;
}
rep(i,siz[left_child[u]]+1){
rep(j,siz[right_child[u]]+1){
dp[u][i+j]=min(dp[u][i+j],dp[left_child[u]][i]+dp[right_child[u]][j]+i*j*val[u]);
dp[u][i+1+j]=min(dp[u][i+1+j],dp[left_child[u]][i]+dp[right_child[u]][j]+val[u]*(i+1)*(j+1));
}
}
return 0;
}
main(){
std::ios::sync_with_stdio(false); cin.tie(NULL);
int t;
iinf*=inf;
cin>>t;
while(t--){
int n,k,i,root;
cin>>n>>k;
rep(i,n){
cin>>a[i];
}
node=0;
root=buildtree(0,n-1);
compute(root);
cout<<dp[root][k]<<endl;
}
return 0;
}
Editorialist's Solution
import java.util.*;
import java.io.*;
class EZRMQ{
//SOLUTION BEGIN
void pre() throws Exception{}
void solve(int TC) throws Exception{
int N = ni(), K = ni();
long[][] best = new long[N][1+N];
for(int i = 0; i< N; i++){
Arrays.fill(best[i], (long)1e17);
best[i][0] = 0;
}
long[] A = new long[N];
for(int i = 0; i< N; i++)A[i] = nl();
int[][] to = new int[N][];
int[] sub = new int[N];
int root = build(to, A, sub, 0, N-1);
fillDP(best, to, sub, A, root);
pn(best[root][K]);
}
void fillDP(long[][] best, int[][] to, int[] sub, long[] A, int u){
//Computing for children
if(to[u][0] != -1)fillDP(best, to, sub, A, to[u][0]);
if(to[u][1] != -1)fillDP(best, to, sub, A, to[u][1]);
int N = A.length;
int lch = to[u][0], rch = to[u][1];
if(lch == -1){
if(rch == -1){
best[u][0] = 0;
best[u][1] = A[u];
}else{
for(int x = 0; x <= sub[rch]; x++){
best[u][x] = Math.min(best[u][x], best[rch][x]);
if(x+1 <= N)best[u][x+1] = Math.min(best[u][x+1], best[rch][x]+(1+x)*A[u]);
}
}
}else {
if(rch == -1){
for(int x = 0; x <= sub[lch]; x++){
best[u][x] = Math.min(best[u][x], best[lch][x]);
if(x+1 <= N)best[u][x+1] = Math.min(best[u][x+1], best[lch][x]+(1+x)*A[u]);
}
}else{
for(int x = 0; x <= sub[lch]; x++){
for(int y = 0; y <= sub[rch]; y++){
best[u][x+y] = Math.min(best[u][x+y], best[lch][x]+best[rch][y]+x*y*A[u]);
best[u][1+x+y] = Math.min(best[u][1+x+y], best[lch][x]+best[rch][y]+(1+x)*(1+y)*A[u]);
}
}
}
}
}
int build(int[][] to, long[] A, int[] sub, int le, int ri){
if(le == ri){
to[le] = new int[]{-1, -1};
sub[le] = 1;
return le;
}
long max = 0;
for(int i = le; i <= ri; i++)max = Math.max(max, A[i]);
if(max == A[le]){
to[le] = new int[]{-1, build(to, A, sub, le+1, ri)};
sub[le] = sub[to[le][1]]+1;
return le;
}
if(max == A[ri]){
to[ri] = new int[]{build(to, A, sub, le, ri-1), -1};
sub[ri] = sub[to[ri][0]]+1;
return ri;
}
for(int i = le+1; i < ri; i++){
if(A[i] == max){
to[i] = new int[]{build(to, A, sub, le, i-1), build(to, A, sub, i+1, ri)};
sub[i] = 1+sub[to[i][0]]+sub[to[i][1]];
return i;
}
}
return -1;
}
//SOLUTION END
void hold(boolean b)throws Exception{if(!b)throw new Exception("Hold right there, Sparky!");}
static boolean multipleTC = true;
FastReader in;PrintWriter out;
void run() throws Exception{
in = new FastReader();
out = new PrintWriter(System.out);
//Solution Credits: Taranpreet Singh
int T = (multipleTC)?ni():1;
pre();for(int t = 1; t<= T; t++)solve(t);
out.flush();
out.close();
}
public static void main(String[] args) throws Exception{
new EZRMQ().run();
}
int bit(long n){return (n==0)?0:(1+bit(n&(n-1)));}
void p(Object o){out.print(o);}
void pn(Object o){out.println(o);}
void pni(Object o){out.println(o);out.flush();}
String n()throws Exception{return in.next();}
String nln()throws Exception{return in.nextLine();}
int ni()throws Exception{return Integer.parseInt(in.next());}
long nl()throws Exception{return Long.parseLong(in.next());}
double nd()throws Exception{return Double.parseDouble(in.next());}
class FastReader{
BufferedReader br;
StringTokenizer st;
public FastReader(){
br = new BufferedReader(new InputStreamReader(System.in));
}
public FastReader(String s) throws Exception{
br = new BufferedReader(new FileReader(s));
}
String next() throws Exception{
while (st == null || !st.hasMoreElements()){
try{
st = new StringTokenizer(br.readLine());
}catch (IOException e){
throw new Exception(e.toString());
}
}
return st.nextToken();
}
String nextLine() throws Exception{
String str = "";
try{
str = br.readLine();
}catch (IOException e){
throw new Exception(e.toString());
}
return str;
}
}
}
Feel free to share your approach. Suggestions are welcomed as always. ![]()
