PROBLEM LINK:
Practice
Contest: Division 1
Contest: Division 2
Setter: Divyanshu Pandey
Tester: Felipe Mota
Editorialist: Taranpreet Singh
DIFFICULTY:
Medium
PREREQUISITES:
Mo’s algorithm on Tree, number theory and Sieve of Eratosthenes.
PROBLEM:
Given a tree with N nodes where value is written at each node. We need to answer queries specifying two nodes u and v, we have to find the number of divisors of the product of values, which lies on the path from u to v.
QUICK EXPLANATION
- If the prime factorization of the product of values on the path from u to v is known we can easily keep track of the number of factors of the product. All we are going to do it to multiply or divide the current product by a prime power and update the number of factors accordingly.
- Reduce the path queries into subarray queries by flattening the tree by the preorder transversal and then apply MO’s algorithm.
EXPLANATION
Let’s assume we just need to find the product and not the number of factors.
For the first 2 subtasks, we can just use BFS or DFS to precompute products for each possible path and answer queries. So focusing only on the final subtask.
In order to solve this, we can flatten the tree into an array in the pre-order transversal of the tree, as follows. This is explained in detail here.
Fix the root of the tree at any node. When we enter a node, we note the start time and add this node to our flattened array, and then recurse into each child. After visiting the subtree of all children, we exit this node, adding this node to flattened array again.
Consider the following tree
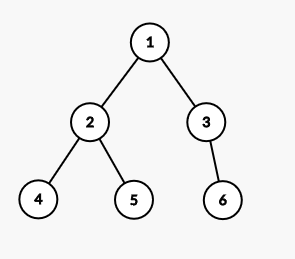
The DFS order would look like 1 2 4 4 5 5 2 3 6 6 3 1 Note that 1 3 6 6 3 2 4 4 5 5 2 1 is also valid. The order of visiting children is irrelevant.
The start time ST and end times ET are as follows
ST(1) = 1, ET(1) = 12
ST(2) = 2, ET(1) = 7
ST(3) = 8, ET(1) = 11
ST(4) = 3, ET(1) = 4
ST(5) = 5, ET(1) = 6
ST(6) = 9, ET(1) = 10
The benefit of this ordering is, suppose we want to consider the nodes on the path from u to v, there are two cases. For generality, assume ST(u) < ST(v), and P is the LCA of u and v
-
P = u
Considering all nodes in range [ST(u), ST(v)]. All nodes on path from u to v appear exactly once in this range. -
P \neq u
Considering all nodes in range [EN(u), ST(v)]. All nodes on the path from u to v except P appear exactly once in this range. We can add the LCA node separately.
Hence, we now have subarray queries, we need to find the product of values in the range. Also, we need to ensure that if a node is already included in the product, we need to exclude it, otherwise, we need to exclude it. We can apply MO’s algorithm to find the product of values on the path. Read more on general Mo’s algorithm here.
Coming back to the original problem, we need to find the number of divisors of the product. If the prime factorization of product is of form \prod p_i^{a_i}, the number of factors of the product is given by \prod (a_i+1)
Let us keep track of the prime factorization of the product. Whenever we add a node into the current interval, let’s decompose current value into prime powers and update the prime factorization as well as the number of the divisor of the updated product. After this, we need to separately handle the LCA node if not included, which can be done manually.
If the updates are still not clear
Suppose the product is 12 = 2^2*3, the number of factors being (2+1)*(1+1) = 6. Suppose we need to update the product by multiplying by 3^2. We first remove all powers of 3, getting product 4 and number of factors as 6/2 = 3 and then multiplying the product by 3^3, giving product 108 and number of factors by (3+1), giving the number of factors as 3*4 = 12
The above idea is sufficient to solve the problem, however, you might get TLE because of large constant factors, especially computing the inverses. Following optimizations might help.
- Precompute the inverses of all numbers from 1 to 20*N instead of calculating it each time during updates. This actually improves the asymptotic time complexity from O(N*\sqrt N * log(MX) * log(MOD)) to O(N*log(MX)*(\sqrt N + log(MOD)) )
- Reducing modular operations as much as possible.
- While sorting intervals in MO’s algorithm, Sorting intervals in the first block in increasing order of endpoints, in the second block by decreasing order of endpoints and so on. See this for details.
TIME COMPLEXITY
The time complexity is O(N*log(MX)*(\sqrt N + log(MOD)) ) per test case.
SOLUTIONS:
Setter's Solution
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define mod 1000000007
#define pb push_back
#define f(a, b) for (ll i = a; i < b; i++)
#define fr(a, b) for (ll j = a; j >= b; j--)
#define fi(a, b) for (ll j = a; j < b; j++)
inline ll mul(ll x, ll y, ll m)
{
ll z = 1LL * x * y;
if (z >= m)
z %= m;
return z;
}
ll n, blockSize, a[100050], b[1000050], m[1000050], p[100050][17], level[100050], in[100050], c,
out[100050], ans[100050], rev[200050], val[200050], cur[200050], inv[2000050], moLeft, moRight;
vector<ll> adj[100050];
vector<pair<ll, ll>> f[1000050];
vector<pair<pair<ll, ll>, pair<pair<ll, ll>, ll>>> query;
void sieve()
{
f(1, 1000050) b[i] = i;
f(2, 1000050) b[i] = 2, i++;
for (ll i = 3; i * i < 1000050; i += 2)
{
if (b[i] == i)
{
for (ll j = i * i; j < 1000050; j += i)
if (b[j] == j)
b[j] = i;
}
}
}
ll powmod(ll x, ll y)
{
ll r = 1;
while (y)
{
if (y & 1)
r = mul(r, x, mod);
y >>= 1;
x = mul(x, x, mod);
}
return r;
}
ll hilbertorder(ll x, ll y)
{
ll maxn = 1LL << 20, logn = 20;
long long d = 0;
for (ll s = 1 << (logn - 1); s; s >>= 1)
{
bool rx = x & s, ry = y & s;
d = d << 2 | rx * 3 ^ static_cast<ll>(ry);
if (!ry)
{
if (rx)
{
x = maxn - x;
y = maxn - y;
}
swap(x, y);
}
}
return d;
}
bool compare(pair<pair<ll, ll>, pair<pair<ll, ll>, ll>> a, pair<pair<ll, ll>, pair<pair<ll, ll>, ll>> b)
{
return a.second.second < b.second.second;
}
void dfs(ll x, ll pr)
{
in[x] = c++;
p[x][0] = pr;
f(0, adj[x].size()) if (adj[x][i] != pr) level[adj[x][i]] = level[x] + 1, dfs(adj[x][i], x);
out[x] = c++;
}
void pre()
{
fi(1, 17)
f(1, n + 1) if (p[i][j - 1] != -1) p[i][j] = p[p[i][j - 1]][j - 1];
}
ll lca(ll u, ll v)
{
if (level[u] > level[v])
swap(u, v);
ll d = level[v] - level[u];
while (d)
{
ll raise = log2(d);
v = p[v][raise];
d -= (1LL << raise);
}
if (u == v)
return u;
fr(16, 0) if (p[u][j] != p[v][j]) u = p[u][j], v = p[v][j];
return p[u][0];
}
vector<pair<ll, ll>> factors(ll x)
{
vector<pair<ll, ll>> fac;
while (x != 1)
{
ll y = b[x], ct = 0;
while (x % y == 0)
x /= y, ct++;
fac.pb({y, ct});
}
return fac;
}
void remove(ll in);
void add(ll in)
{
if (cur[rev[in]] & 1)
{
remove(in);
return;
}
cur[rev[in]] ^= 1;
ll v = val[in];
if (v == 1)
return;
if (f[v].size() == 0)
f[v] = factors(v);
f(0, f[v].size())
{
c = mul(c, inv[m[f[v][i].first] + 1], mod),
c = mul(c, f[v][i].second + m[f[v][i].first] + 1, mod),
m[f[v][i].first] += f[v][i].second;
}
}
void remove(ll in)
{
if (!(cur[rev[in]] & 1))
{
add(in);
return;
}
cur[rev[in]] ^= 1;
ll v = val[in];
if (v == 1)
return;
if (f[v].size() == 0)
f[v] = factors(v);
f(0, f[v].size())
{
c = mul(c, inv[m[f[v][i].first] + 1], mod),
c = mul(c, m[f[v][i].first] - f[v][i].second + 1, mod),
m[f[v][i].first] -= f[v][i].second;
}
}
void moQuery(ll l, ll r)
{
while (moLeft < l)
remove(moLeft++);
while (moLeft > l)
add(--moLeft);
while (moRight < r)
add(++moRight);
while (moRight > r)
remove(moRight--);
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("input.txt", "rt", stdin);
freopen("output.txt", "wt", stdout);
#endif
ios_base::sync_with_stdio(false);
cin.tie(NULL);
sieve();
f(0, 2000050) inv[i] = powmod(i, mod - 2);
ll t, x, y;
cin >> t;
while (t--)
{
memset(m, 0, sizeof(m));
memset(p, -1, sizeof(p));
memset(cur, 0, sizeof(cur));
query.clear();
cin >> n;
blockSize = sqrt(n);
f(0, n + 2) adj[i].clear();
f(0, n - 1) cin >> x >> y, adj[x].pb(y), adj[y].pb(x);
f(1, n + 1) cin >> a[i];
c = 1;
dfs(1, -1);
f(1, n + 1) val[in[i]] = val[out[i]] = a[i], rev[in[i]] = rev[out[i]] = i;
pre();
ll q;
cin >> q;
f(1, q + 1)
{
cin >> x >> y;
ll k = lca(x, y);
if (k != x && k != y)
{
if (out[x] < in[y])
query.pb({{out[x], in[y]}, {{in[k], i}, hilbertorder(out[x], in[y])}});
else
query.pb({{out[y], in[x]}, {{in[k], i}, hilbertorder(out[y], in[x])}});
}
else
{
if (k == x)
query.pb({{in[x], in[y]}, {{-1, i}, hilbertorder(in[x], in[y])}});
else
query.pb({{in[y], in[x]}, {{-1, i}, hilbertorder(in[y], in[x])}});
}
}
sort(query.begin(), query.end(), compare);
c = 1;
moLeft = 1, moRight = 0;
f(0, query.size())
{
ll l = query[i].first.first,
r = query[i].first.second,
lca = query[i].second.first.first,
in = query[i].second.first.second;
moQuery(l, r);
ll currentAns = c;
if (lca != -1)
add(lca), currentAns = c, remove(lca);
ans[in] = currentAns;
}
f(1, q + 1) cout << ans[i] << "\n";
}
return 0;
}
Tester's Solution
//Please change code to handle multiple tests
#include <bits/stdc++.h>
using namespace std;
template<typename T = int> vector<T> create(size_t n){ return vector<T>(n); }
template<typename T, typename... Args> auto create(size_t n, Args... args){ return vector<decltype(create<T>(args...))>(n, create<T>(args...)); }
struct forest {
vector<pair<int,int>> edges;
vector<vector<int>> to, lg_parents;
vector<int> sub, color, parent, depth, pre, ord, in, out, bi_ord;
int comps, n, lgn, C;
forest(int n): n(n) {
to.resize(n);
sub.assign(n, 0);
color.assign(n, 0);
parent.resize(n);
depth.assign(n, 0);
in.resize(n);
out.resize(n);
}
void add_edge(int u, int v){
int id = edges.size();
assert(id < n - 1);
edges.push_back(make_pair(u, v));
to[u].push_back(id);
to[v].push_back(id);
}
inline int adj(int u, int id){ return u ^ edges[id].first ^ edges[id].second; }
void dfs(int u, int p){
bi_ord.push_back(u);
pre.push_back(u);
in[u] = C++;
color[u] = comps;
parent[u] = p;
sub[u] = 1;
for(int id : to[u]){
int v = adj(u, id);
if(v == p) continue;
depth[v] = depth[u] + 1;
dfs(v, u);
sub[u] += sub[v];
}
out[u] = C;
bi_ord.push_back(u);
ord.push_back(u);
}
bool is_ancestor(int u, int v){
return in[u] <= in[v] && out[v] <= out[u];
}
void dfs_all(){
comps = 0;
C = 0;
for(int i = 0; i < n; i++){
if(!color[i]){
++comps;
dfs(i, -1);
}
}
}
void build_parents(){
lgn = 0;
while((1<<lgn) <= n) lgn++;
lg_parents.assign(lgn, vector<int>(n, -1));
for(int i = 0; i < n; i++)
lg_parents[0][i] = parent[i];
for(int i = 1; i < lgn; i++){
for(int j = 0; j < n; j++){
if(~lg_parents[i - 1][j]){
lg_parents[i][j] = lg_parents[i - 1][lg_parents[i - 1][j]];
}
}
}
}
int jump(int u, int k){
for(int i = lgn - 1; i >= 0; i--) if(k&(1<<i)) u = lg_parents[i][u];
return u;
}
int lca(int u, int v){
if(depth[u] < depth[v]) swap(u, v);
for(int i = lgn - 1; i >= 0; i--)
if((depth[u] - depth[v])&(1<<i))
u = lg_parents[i][u];
if(u == v)
return u;
for(int i = lgn - 1; i >= 0; i--)
if(lg_parents[i][u] != lg_parents[i][v]){
u = lg_parents[i][u];
v = lg_parents[i][v];
}
return lg_parents[0][u];
}
int dist(int u, int v){
return depth[u] + depth[v] - 2 * depth[lca(u, v)];
}
};
template<typename T = int, T mod = 1'000'000'007, typename U = long long>
struct umod{
T val;
umod(): val(0){}
umod(U x){ x %= mod; if(x < 0) x += mod; val = x;}
umod& operator += (umod oth){ val += oth.val; if(val >= mod) val -= mod; return *this; }
umod& operator -= (umod oth){ val -= oth.val; if(val < 0) val += mod; return *this; }
umod& operator *= (umod oth){ val = ((U)val) * oth.val % mod; return *this; }
umod& operator /= (umod oth){ return *this *= oth.inverse(); }
umod& operator ^= (U oth){ return *this = pwr(*this, oth); }
umod operator + (umod oth) const { return umod(*this) += oth; }
umod operator - (umod oth) const { return umod(*this) -= oth; }
umod operator * (umod oth) const { return umod(*this) *= oth; }
umod operator / (umod oth) const { return umod(*this) /= oth; }
umod operator ^ (long long oth) const { return umod(*this) ^= oth; }
bool operator < (umod oth) const { return val < oth.val; }
bool operator > (umod oth) const { return val > oth.val; }
bool operator <= (umod oth) const { return val <= oth.val; }
bool operator >= (umod oth) const { return val >= oth.val; }
bool operator == (umod oth) const { return val == oth.val; }
bool operator != (umod oth) const { return val != oth.val; }
umod pwr(umod a, U b) const { umod r = 1; for(; b; a *= a, b >>= 1) if(b&1) r *= a; return r; }
umod inverse() const {
U a = val, b = mod, u = 1, v = 0;
while(b){
U t = a/b;
a -= t * b; swap(a, b);
u -= t * v; swap(u, v);
}
if(u < 0)
u += mod;
return u;
}
};
using U = umod<>;
const int LIM = 1'000'001;
int prime[LIM], active[LIM], cnt[LIM];
int x_prs[LIM][20], y_prs[LIM][20], stk_prs[LIM];
const int LIM_INVS = LIM * 2;
U invs[LIM_INVS];
int main(){
/**
* We can use mos on tree trick and solve the problem in complexity O(N sqrt N log MaxA)
*
* Keep a global variable with the number of times each prime appears as a factor in the
* decomposition of numbers in the path, keep the path updated with mos, the answer to a
* query is the multiplication of all such values.
* */
ios::sync_with_stdio(false);
cin.tie(0);
const int mod = 1'000'000'007;
invs[1] = 1;
for(int i = 2; i < LIM_INVS; i++)
invs[i] -= (U(mod / i) * invs[mod % i]);
int n; cin >> n;
forest fo(n);
for(int i = 1; i < n; i++){
int u, v; cin >> u >> v; u--; v--;
fo.add_edge(u, v);
}
vector<int> vals(n);
for(int i = 0; i < n; i++){
cin >> vals[i];
active[vals[i]] = 1;
}
for(int i = 2; i < LIM; i++){
if(!prime[i]){
for(int j = i; j < LIM; j += i){
prime[j] = 1;
if(active[j]){
int k = j, c = 0;
while(k % i == 0){
c++;
k /= i;
}
x_prs[j][stk_prs[j]] = i;
y_prs[j][stk_prs[j]] = c;
stk_prs[j]++;
}
}
}
}
fo.dfs_all();
fo.build_parents();
vector<int> st(n), ed(n);
for(int i = 0; i < 2 * n; i++) ed[fo.bi_ord[i]] = i;
for(int i = 2 * n; i >= 0; i--) st[fo.bi_ord[i]] = i;
struct query {
int id, l, r, lca;
};
int sq = 1;
while(sq * sq < n) sq++;
vector<int> bl(2 * n);
for(int i = 0; i < 2 * n; i++) bl[i] = i / sq;
vector<query> queries;
int q; cin >> q;
vector<int> ans(q);
for(int i = 0; i < q; i++){
int u, v; cin >> u >> v; u--; v--;
if(st[u] > st[v]) swap(u, v);
query now;
now.id = i;
int lca = fo.lca(u, v);
if(lca == u) now.l = st[u], now.r = st[v];
else now.l = ed[u], now.r = st[v];
now.lca = lca;
queries.push_back(now);
}
sort(queries.begin(), queries.end(), [&](query a, query b){
if(bl[a.l] != bl[b.l]) return bl[a.l] < bl[b.l];
if(bl[a.l] % 2) return a.r < b.r;
return a.r > b.r;
});
vector<int> appears(n);
for(int i = 0; i < LIM; i++) cnt[i] = 1;
U res = 1;
auto update = [&](int u){
int d = (appears[u] == 0) ? 1 : -1;
int v = vals[u], len = stk_prs[vals[u]];
for(int i = 0; i < len; i++){
int p = x_prs[v][i], c = y_prs[v][i];
res *= invs[cnt[p]];
cnt[p] += d * c;
res *= cnt[p];
}
appears[u] ^= 1;
};
int l = 0, r = -1;
for(auto qr : queries){
while(l > qr.l) update(fo.bi_ord[--l]);
while(r < qr.r) update(fo.bi_ord[++r]);
while(l < qr.l) update(fo.bi_ord[l++]);
while(r > qr.r) update(fo.bi_ord[r--]);
int u = fo.bi_ord[qr.l], v = fo.bi_ord[qr.r];
if(u != qr.lca && v != qr.lca) update(qr.lca);
ans[qr.id] = res.val;
if(u != qr.lca && v != qr.lca) update(qr.lca);
}
for(int v : ans)
cout << v << '\n';
return 0;
}
Editorialist's Solution
import java.util.*;
import java.io.*;
import java.text.*;
class FCTRE{
//SOLUTION BEGIN
long MOD = (long)1e9+7;
void pre() throws Exception{}
void solve(int TC) throws Exception{
int n = ni();ti = -1;
int[] from = new int[n-1], to = new int[n-1];
for(int i = 0; i< n-1; i++){
from[i] = ni()-1;
to[i] = ni()-1;
}
int[][] g = make(n, from, to, n-1, true);
int[] a = new int[n];
for(int i = 0; i< n; i++)a[i] = ni();
LCA lca = new LCA(g);
int[] eu = new int[2*n];
int[] st = new int[n], en = new int[n];
dfs(g, st, en, eu, 0, -1);
int mx = (int)1e6+1;
int[] spf = new int[mx];
long[] inv = new long[20*n];
for(int i = 1; i< inv.length; i++)inv[i] = inv(i);
for(int i = 2; i< mx; i++)
if(spf[i] == 0)
for(int j = i; j< mx; j+=i)
if(spf[j] == 0)
spf[j] = i;
int q = ni();
int[][] qu = new int[q][];
for(int i = 0; i< q; i++){
int u = ni()-1, v = ni()-1;
if(st[u] > st[v]){
int tmp = u;u=v;v=tmp;
}
int l = lca.lca(u, v);
if(u == l)qu[i] = new int[]{i, st[u], st[v], -1};
else qu[i] = new int[]{i, en[u], st[v], l};
}
int B = 500;
Arrays.sort(qu, (int[] i1, int[] i2) -> {
if(i1[1]/B == i2[1]/B)return Integer.compare(i1[2], i2[2])*((i1[1]/B)%2 == 0?1:-1);
return Integer.compare(i1[1], i2[1]);
});
int[] f = new int[mx];
Arrays.fill(f, 1);
long[] ans = new long[q];
long cur = 1;
int le = 0, ri = -1;
byte[] added = new byte[n];
for(int i = 0; i< q; ++i){
while(ri < qu[i][2]){
++ri;
int u = eu[ri];
int x = a[u];
while(x>1){
int p = spf[x];int cnt = 0;
while(x%p == 0){x/=p;cnt++;}
cur = (cur*inv[f[p]])%MOD;
int delta = (added[u] == 0?1:-1);
f[p] += delta*cnt;
cur = (cur*f[p])%MOD;
}
added[u] ^= 1;
}
while(le > qu[i][1]){
--le;
int u = eu[le];
int x = a[u];
while(x>1){
int p = spf[x];int cnt = 0;
while(x%p == 0){x/=p;cnt++;}
cur = (cur*inv[f[p]])%MOD;
int delta = (added[u] == 0?1:-1);
f[p] += delta*cnt;
cur = (cur*f[p])%MOD;
}
added[u] ^= 1;
}
while(ri > qu[i][2]){
int u = eu[ri];
int x = a[u];
while(x>1){
int p = spf[x];int cnt = 0;
while(x%p == 0){x/=p;cnt++;}
cur = (cur*inv[f[p]])%MOD;
int delta = (added[u] == 0?1:-1);
f[p] += delta*cnt;
cur = (cur*f[p])%MOD;
}
added[u] ^= 1;
--ri;
}
while(le < qu[i][1]){
int u = eu[le];
int x = a[u];
while(x>1){
int p = spf[x];int cnt = 0;
while(x%p == 0){x/=p;cnt++;}
cur = (cur*inv[f[p]])%MOD;
int delta = (added[u] == 0?1:-1);
f[p] += delta*cnt;
cur = (cur*f[p])%MOD;
}
added[u] ^= 1;
++le;
}
long fact = 1;
if(qu[i][3] != -1){
int u = qu[i][3];
int x = a[u];
while(x>1){
int p = spf[x];int cnt = 0;
while(x%p == 0){x/=p;cnt++;}
fact = (fact*inv[f[p]])%MOD;
fact = (fact*(f[p]+cnt))%MOD;
}
}
ans[qu[i][0]] = (cur*fact)%MOD;
}
for(long l:ans)pn(l);
}
long inv(long x){return pow(x, MOD-2);}
long pow(long a, long p){
long o = 1;
for(;p>0;p>>=1){
if((p&1)==1)o = (o*a)%MOD;
a = (a*a)%MOD;
}
return o;
}
int ti = -1;
void dfs(int[][] g, int[] st, int[] en, int[] eu, int u, int p){
eu[++ti] = u;
st[u] = ti;
for(int v:g[u])if(v != p)dfs(g, st, en, eu, v, u);
eu[++ti] = u;
en[u] = ti;
}
final class LCA{
int n = 0, ti= -1;
int[] eu, fi, d;
RMQ rmq;
public LCA(int[][] g){
n = g.length;
eu = new int[2*n-1];fi = new int[n];d = new int[n];
Arrays.fill(fi, -1);Arrays.fill(eu, -1);
dfs(g, 0, -1);
rmq = new RMQ(eu, d);
}
void dfs(int[][] g, int u, int p){
eu[++ti] = u;fi[u] = ti;
for(int v:g[u])if(v!=p){
d[v] = d[u]+1;
dfs(g, v, u);eu[++ti] = u;
}
}
int lca(int u, int v){return rmq.query(Math.min(fi[u], fi[v]), Math.max(fi[u], fi[v]));}
int dist(int u, int v){return d[u]+d[v]-2*d[lca(u,v)];}
class RMQ{
int[] len, d;
int[][] rmq;
public RMQ(int[] ar, int[] weight){
len = new int[ar.length+1];
this.d = weight;
for(int i = 2; i<= ar.length; i++)len[i] = len[i>>1]+1;
rmq = new int[len[ar.length]+1][ar.length];
for(int i = 0; i< rmq.length; i++)
for(int j = 0; j< rmq[i].length; j++)
rmq[i][j] = -1;
for(int i = 0; i< ar.length; i++)rmq[0][i] = ar[i];
for(int b = 1; b<= len[ar.length]; b++)
for(int i = 0; i + (1<<b)-1< ar.length; i++)
if(weight[rmq[b-1][i]]<weight[rmq[b-1][i+(1<<(b-1))]])rmq[b][i] =rmq[b-1][i];
else rmq[b][i] = rmq[b-1][i+(1<<(b-1))];
}
int query(int l, int r){
if(l==r)return rmq[0][l];
int b = len[r-l];
if(d[rmq[b][l]]<d[rmq[b][r-(1<<b)]])return rmq[b][l];
return rmq[b][r-(1<<b)];
}
}
}
int[][] make(int n, int[] from, int[] to, int e, boolean f){
int[][] g = new int[n][];int[]cnt = new int[n];
for(int i = 0; i< e; i++){
cnt[from[i]]++;if(f)cnt[to[i]]++;
}
for(int i = 0; i< n; i++)g[i] = new int[cnt[i]];
for(int i = 0; i< e; i++){
g[from[i]][--cnt[from[i]]] = to[i];
if(f)g[to[i]][--cnt[to[i]]] = from[i];
}
return g;
}
//SOLUTION END
void hold(boolean b)throws Exception{if(!b)throw new Exception("Hold right there, Sparky!");}
DecimalFormat df = new DecimalFormat("0.00000000000");
static boolean multipleTC = true;
FastReader in;PrintWriter out;
void run() throws Exception{
in = new FastReader();
out = new PrintWriter(System.out);
//Solution Credits: Taranpreet Singh
int T = (multipleTC)?ni():1;
pre();for(int t = 1; t<= T; t++)solve(t);
out.flush();
out.close();
}
public static void main(String[] args) throws Exception{
new FCTRE().run();
}
int bit(long n){return (n==0)?0:(1+bit(n&(n-1)));}
void p(Object o){out.print(o);}
void pn(Object o){out.println(o);}
void pni(Object o){out.println(o);out.flush();}
String n()throws Exception{return in.next();}
String nln()throws Exception{return in.nextLine();}
int ni()throws Exception{return Integer.parseInt(in.next());}
long nl()throws Exception{return Long.parseLong(in.next());}
double nd()throws Exception{return Double.parseDouble(in.next());}
class FastReader{
BufferedReader br;
StringTokenizer st;
public FastReader(){
br = new BufferedReader(new InputStreamReader(System.in));
}
public FastReader(String s) throws Exception{
br = new BufferedReader(new FileReader(s));
}
String next() throws Exception{
while (st == null || !st.hasMoreElements()){
try{
st = new StringTokenizer(br.readLine());
}catch (IOException e){
throw new Exception(e.toString());
}
}
return st.nextToken();
}
String nextLine() throws Exception{
String str = "";
try{
str = br.readLine();
}catch (IOException e){
throw new Exception(e.toString());
}
return str;
}
}
}
Feel free to share your approach. Suggestions are welcomed as always. ![]()
