In the question it is not written that we have to make the permutation with the natural numbers starting from 1 and ending at ‘n’. We can make permutation of any numbers, isn’t it? And it is also written that if multiple permutation are possible, output any of them.
Question Link
If you agree with me, then please see that, shouldn’t my answer be correct?!
My Solution to the problem
P.S.- Please @admin, guide me.
1 Like
By definition, A permutation is a sequence of integers from 1 to n of length n containing each number exactly once.
Since it was mentioned that we have to make a permutation, it itself implies that we have to make it with the natural numbers starting from 1 and ending at ‘n’.
I think this will help you:
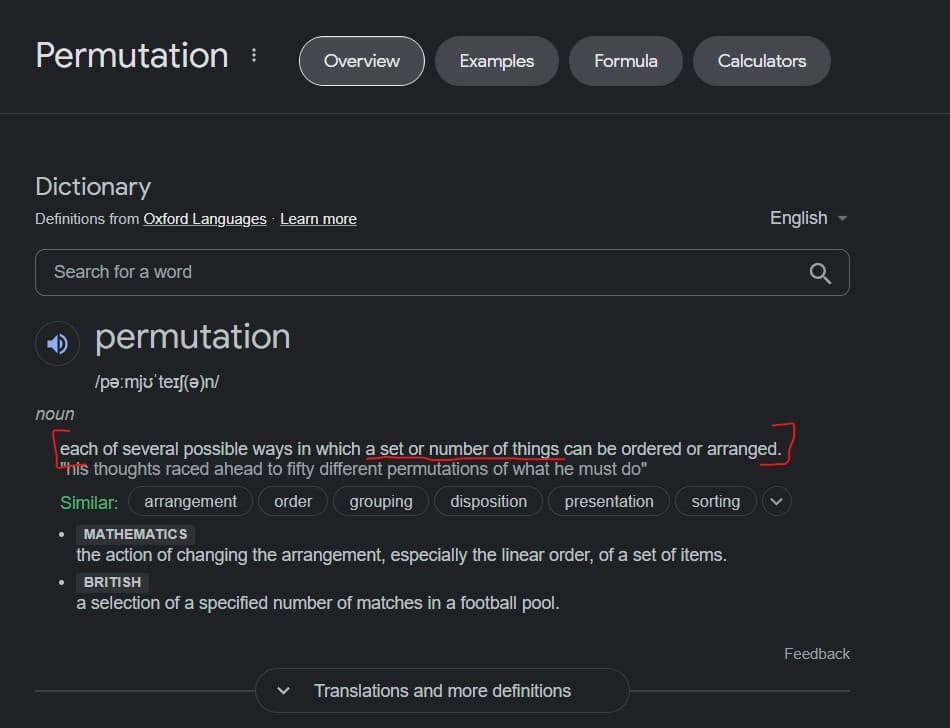
Permutation is arrangement of a set or number of things, in the question its not written anything like, permutation of set of first N natural numbers.
So, its not clear from the question that we have to take the first N natural numbers for the permutation, we can take any set of numbers.
If I am wrong, then please correct me!
1 Like
People in the problem setting panel were really careless about it. How can one assume the word Permutation as an arrangement of numbers from 1 to N?
1 Like
+1