FIBOSEQ - Editorial

editorial
, , , , ,
1

PROBLEM LINK:

Contest - Division 3
Contest - Division 2
Contest - Division 1

DIFFICULTY:

EASY-MEDIUM

PREREQUISITES:

Dynamic Programming, Binary Exponentiation, Fermats Little Theorem

PROBLEM:

Define the sequence f_i as:

  • f_0 = \text{``0"}
  • f_1 = \text{``1"}
  • f_i = f_{i-1}+f_{i-2} for i\ge 2, where + is the string concatenation operation.

Determine the sum of the digits of all subsequences of f_i modulo 10^9+7.

EXPLANATION:

It is evident that f_i only consists of zeros and ones. Let k_i denote the number of ones in f_i.
Also, let len_i denote the length of string f_i.

Claim: Every digit in f_i occurs in exactly 2^{len_i-1} subsequences of f_i.
(See this for details. Complete proof is trivial and left to the reader.)

The sum of the digits over all subsequences is equivalent to the sum of the number of times each 1 occurs in a subsequence. From the above claim, it is clear that the answer is then k_i*2^{len_i-1}.

All that remains is to calculate k_i and len_i efficiently.

Since f_i is the concatenation of f_{i-1} and f_{i-1}, k_i is therefore equal to k_{i-1}+k_{i-2}. Similarly, len_i is equal to len_{i-1}+len_{i-2}. This can be precomputed quickly using dynamic programming.

Recurrence relations

The formula for calculating k_i is

  • k_0 = 0, k_1 = 1
  • k_i = k_{i-1}+k_{i-2}

Similarly, the formula for calculating len_i is

  • len_0 = 1, len_1 = 1
  • len_i = len_{i-1}+len_{i-2}

Special emphasis must be made on the method to compute the answer modulo MOD = 10^9+7.
The important point to note here is that, while computing the answer modulo MOD,

k_i*2^{len_i-1} \equiv (k_i\%MOD)*(2^{(len_i-1)\%(MOD-1)}\%MOD) \mod{MOD}

(not 2^{(len_i-1) \% MOD}) by application of Fermats little theorem (see this for details).
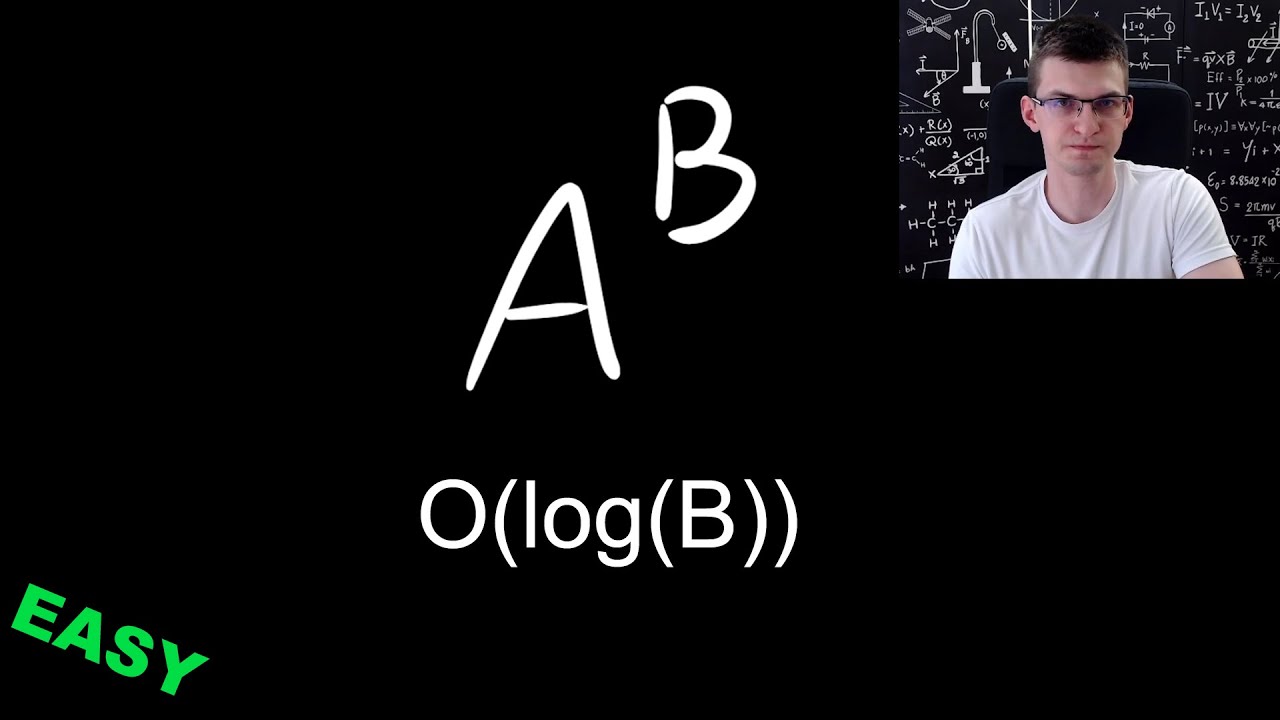
You should use binary exponentiation to compute the value of 2^{len_i} in O(\log len_i).

TIME COMPLEXITY:

Precomputing the answer for every i \le 10^5 can be done in

O(n*log(MOD))

where MOD=10^9+7. The \log factor is present because of the pow function (which implements binary exponentiation for an optimal runtime).

SOLUTIONS:

Editorialist’s solution can be found here.

BONUS:

How would you find the sum of digits over all subsequences of f_i when i \le 10^{18}?

Experimental: For evaluation purposes, please rate the editorial (1 being poor and 5 excellent)

  • 1
  • 2
  • 3
  • 4
  • 5

0 voters

3 Likes
2

I liked the problem honestly, the idea wasn’t tricky but I had 2 approaches which failed due to the use of modulo, which I didn’t expect. I was able to debug it during the contest time so I’ll count it as a great learning experience :).

As for the bonus part, matrix exponentiation works doesn’t it?

6 Likes
3

why can’t we do this way ??
Solution: 49948250 | CodeChef

1 Like
4

Doing 2^P \mod (10^9 + 7) is not the same as doing 2^{(P \mod (10^9 + 7))}\mod (10^9 + 7) which causes issues in your case. I made the same mistake multiple times.

3 Likes
5

\mathcal{O}(\log N) solution (Bonus)

7 Likes
7

Better really to recursively compute the number of subsequences to which each element belongs, taking the mod at each step. That way there’s no need for number theory on exponents (nor any reliance on the modulus being prime, although it is of course).

Since len_i = len_{i-1} + len_{i-2}, we can calculate that each element’s subsequence membership count e_i = 2^{len_{i}}/2 = e_{i-1} * e_{i-2} * 2. And we can just take \mod 1000000007 at each step.

Python implementation using this

8

Any idea why this is wrong? (init runs before solve)

const int MOD = 1e9 + 7;

vll fib(1e5 + 5);
void init() {
  fib[0] = 0, fib[1] = 1;
  fo(i, 2, SZ(fib)) fib[i] = (fib[i - 1] + fib[i - 2]) % MOD;
}

ll get_ones(int i) { return fib[i]; }
ll get_length(int i) { return fib[i + 1]; }

ll modpow(ll a, ll b) {
  ll ans = 1;
  while (b > 0) {
    if (b % 2 == 1) {
      ans *= a;
      ans %= MOD;
    }
    a *= a;
    a %= MOD;
    b /= 2;
  }
  return ans;
}

void solve(int testcase) {
  int n;
  cin >> n;

  ll k = get_ones(n), l = get_length(n);
  ll res = (k * modpow(2, l - 1)) % MOD;

  cout << res << '\n';
}
9

I assume you have done this using matrix exponentiation. Could you say what’s wrong in my code??

code

10

you need to take the mod properly while calculating res in solve function.

try this
→ res = k * modpow(2 , (l-1) % (mod-1)) % mod;

11

So every time I compute a^x mod p , I need to use Fermats little theorem (given p is prime ) ?
Though I have calculated a^x mod p directly is various problems and didn’t got WA , can you please differentiate where should I use the either one? I am new to this topic.

12

Here are nice videos by @errichto on Binary Exponentiation and Modular Arithmetic I watched yesterday. They are really useful, although nothing specific about Fermat’s theorem was explained in the video.