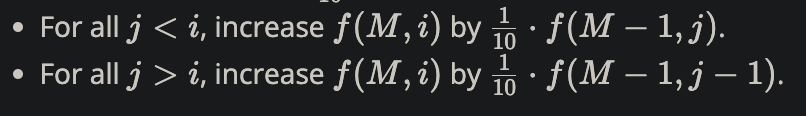PROBLEM LINK:
Practice
Contest: Division 1
Contest: Division 2
Contest: Division 3
Contest: Division 4
Author:
Tester: apoorv_me
Editorialist: iceknight1093
DIFFICULTY:
Easy - Medium
PREREQUISITES:
Dynamic Programming
PROBLEM:
You have a digit string, with some digits replaced by ?.
Repeat the following while the string contains a \text{'?'}:
- Randomly choose a digit from 0 to 9.
- Then, replace one occurrence of \text{'?'} with this digit.
Your aim is to maximize the integer represented by the digit string.
Find the expected final value of each digit of the string.
EXPLANATION:
The \text{'?'} will be referred to as “blank spaces” below.
First, note that any non-blank spaces in the string will keep their values, so we can ignore them entirely.
If there are M blank spaces in the string, we essentially have a string of length M, filled with blanks, to deal with now.
Let f(M, i) denote the expected value of the i-th digit.
We’ll try to analyze what we’ll do once we obtain the first digit, say d.
Suppose we decide to place it at position i.
Then, for the other indices:
- For j \lt i, the expected value of the j-th digit is now f(M-1, j).
- For j \gt i, the expected value of the j-th digit is now f(M-1, j-1).
This is because once the first digit is placed, we functionally have a blank string of length M-1 to work with.
In particular, note that the index i must satisfy f(M-1, i) \leq d, because if f(M-1, i) \gt d then it’s better to place d at a later index and leave i blank instead.
This in fact immediately tells us what i should be: it’s ideally going to be the leftmost index such that f(M-1, i) \leq d.
This allows us to compute all the f(M, i) values using dynamic programming.
First, fix the digit d that’s drawn. Each of them have a 10\% chance of showing up.
Once d is fixed, find the leftmost index i such that f(M-1, i) \leq d.
Then,
- Increase f(M, i) by \frac d {10}.
- For all j \lt i, increase f(M, j) by \frac 1 {10} \cdot f(M-1, j).
- For all j \gt i, increase f(M,j) by \frac 1 {10} \cdot f(M-1, j-1).
Since we only consider 0 \leq d \leq 9, and each of them requires \mathcal{O}(M) work, all the f(M, i) values can be found in \mathcal{O}(10M) time once all the f(M-1, i) values are known.
So, starting with f(1, 1) = 4.5, building up all the f(M, i) values can be done in \mathcal{O}(10 M^2) time, which is fast enough since M \leq N \leq 2000.
Once these are known, we know the expected value of each blank space of the original string; and the expected value at each non-blank space is of course the digit itself.
TIME COMPLEXITY:
\mathcal{O}(10\cdot N^2) per testcase.
CODE:
Author's code (C++)
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define INF (int)1e18
mt19937_64 RNG(chrono::steady_clock::now().time_since_epoch().count());
void Solve()
{
int n; cin >> n;
string s; cin >> s;
vector<vector<double>> dp(n + 1, vector<double>(n + 1, 0.0));
dp[1][1] = 4.5;
for (int i = 2; i <= n; i++){
int p = 1;
for (int j = 9; j >= 0; j--){
// should we put at p or p + 1?
// check where expected value of position p is larger
while (p < i && dp[i - 1][p] > j){
p++;
}
// with probability 0.1 add this to all places
for (int k = 1; k <= n; k++){
if (k < p){
dp[i][k] += dp[i - 1][k] * 0.1;
} else if (k == p){
dp[i][k] += j * 0.1;
} else {
dp[i][k] += dp[i - 1][k - 1] * 0.1;
}
}
}
}
int m = 0;
for (auto x : s){
m += (x == '?');
}
int p = 0;
for (int i = 0; i < n; i++){
double ans;
if (s[i] == '?'){
ans = dp[m][++p];
} else {
ans = (s[i] - '0');
}
cout << fixed << setprecision(8) << ans << " \n"[i + 1 == n];
}
}
int32_t main()
{
auto begin = std::chrono::high_resolution_clock::now();
ios_base::sync_with_stdio(0);
cin.tie(0);
int t = 1;
// freopen("in", "r", stdin);
// freopen("out", "w", stdout);
cin >> t;
for(int i = 1; i <= t; i++)
{
//cout << "Case #" << i << ": ";
Solve();
}
auto end = std::chrono::high_resolution_clock::now();
auto elapsed = std::chrono::duration_cast<std::chrono::nanoseconds>(end - begin);
cerr << "Time measured: " << elapsed.count() * 1e-9 << " seconds.\n";
return 0;
}
Editorialist's code (Python3)
for _ in range(int(input())):
n = int(input())
s = input()
m = s.count('?')
dp = [ [0 for _ in range(m)] for _ in range(m)]
dp[0][0] = 4.5
for i in range(1, m):
for d in range(0, 10):
done = 0
for j in range(0, i+1):
if done: dp[i][j] += 0.1 * dp[i-1][j-1]
else:
if j == i or d >= dp[i-1][j]:
done = 1
dp[i][j] += 0.1 * d
else:
dp[i][j] += 0.1 * dp[i-1][j]
x = 0
ans = []
for i in range(n):
if s[i] == '?':
ans.append(dp[-1][x])
x += 1
else: ans.append(s[i])
print(*ans)