Problem Link : CodeChef: Practical coding for everyone
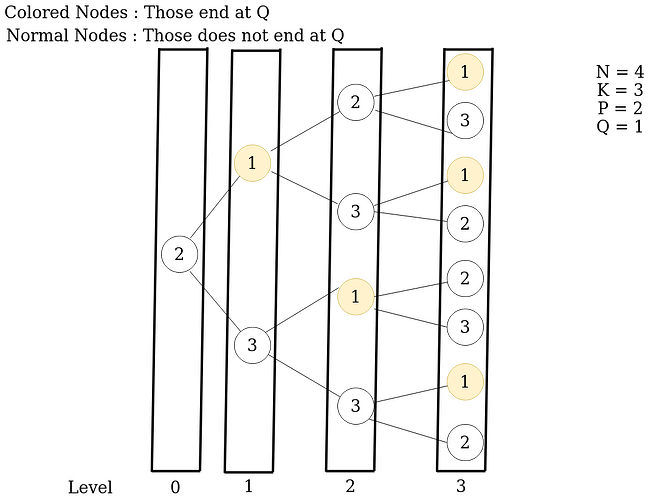
Let A be the array that consist of number of nodes ending at Q at a particular level
A = { 0, 1 , 1, 3 }
Let B be the array that consist of number of nodes NOT ending at Q at a particular level
B = {1, 1 , 3, 5 }
Convention : Favourable nodes ( ending at Q )
Non Favourable nodes (NOT ending at Q)
On carefull observation it may be noted that:
-
A[i] = B[i-1]
Reason :
All the favourable nodes ( ending at Q ) will only be produced by non favourable nodes of the previous level. -
B[i] = A[i-1] X (K – 1) + B[i-1] X (K – 2)
Reason :
a) For A[i-1]*(K – 1) , some of the non favourable nodes are produced by favourable nodes of the previous level , multiply by (K – 1 ) as each favourable node will produce K-1 non favourable nodes
b) For B[i-1]*(K – 2) , rest of the non favourable nodes are produced by non favourable nodes of previous level, multiply by (K-2) , as one produced node is favourable, so we subtract 2 from this.
#include <bits/stdc++.h>
using namespace std;
#define MOD 1000000007
class element
{
public:
long long int a;
long long int b;
};
int main()
{ long long int test;
cin >> test;
while(test--){
long long int n, k, p, q;
cin >> n >> k >> p >> q;
element *dp = new element[n];
// if the number of balls in the first box is same as in the last box
// then
if (p == q)
{
dp[0].a = 1;
dp[0].b = 0;
}
else
{
dp[0].a = 0;
dp[0].b = 1;
}
// dp approach as mentioned in the text
for (int i = 1; i < n; i++)
{
dp[i].a = dp[i - 1].b;
dp[i].b = (dp[i - 1].a * (k - 1)) % MOD + (dp[i - 1].b * (k - 2)) % MOD;
dp[i].b %= MOD;
}
cout << dp[n - 1].a << endl;
}
}