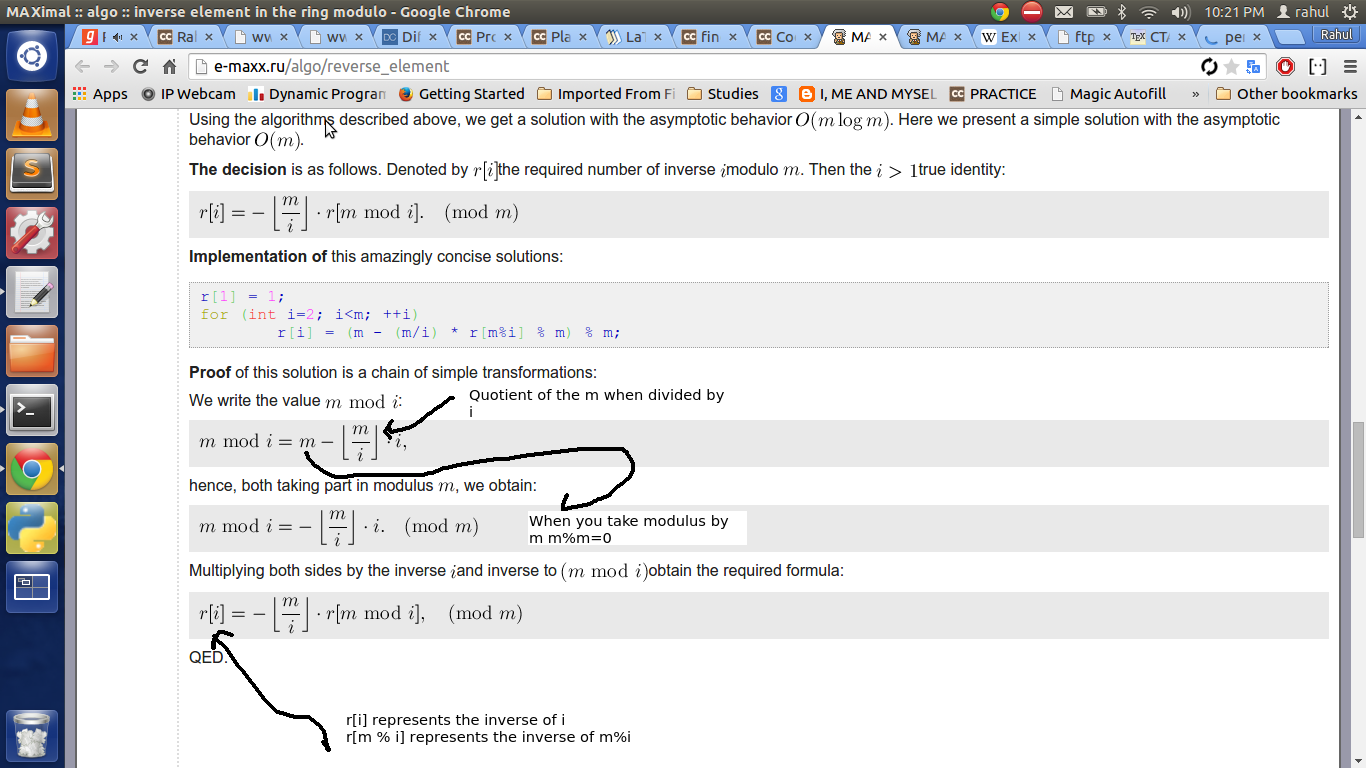
While searching about inverse modulo, i got to know about a concise algorithm to find inverse modulo of
numbers in range[1…n) under modulo m.
Time complexity of this approach is O(n).
Implementation of the algorithm:
r[1] = 1;
for (int i=2; i<n; ++i)
r[i] = (m - (m/i) * r[m%i] % m) % m;
Here is the link:
http://e-maxx.ru/algo/reverse_element
I am unable to understand the proof of the algorithm.
It would be very helpful if anyone explains the same in a simple way.