A group of friends live in a “square” city having only “vertical” streets (with numbers from 0 to 100000 from extreme west to extremely eastern) and “horizontal” streets (with numbers from 0 to 100000 from extremely southern to extremely northern). The distances between adjacent “vertical” streets are 1, similar to “horizontal” streets. Friends decided to meet at the one of them who would be closest to the others, i.e. the total length of roads of all friends from places of residence to the meeting host would be minimal. Each friend lives at the intersection of a certain vertical and horizontal street and intends to go to the party by the shortest route, but only through the streets.
Task:
Write a program that calculates the total length of roads (the smallest possible) that friends must travel to meet at the meeting’s host.
Input:
In the first line, the standard selection is the integer Z (1 <= Z <= 50) In a series of lines, Z data sets are recorded, which are in accordance with the specifications given below. One data set The first row is written by the number of friends N (1 ≤ N ≤ 10,000). In lines 2 … N + 1 are written friends in the form of numerical numbers xi, separated by a space. The number x_i means the number of the vertical street, and yi the number of the horizontal street on which the ith friends live, (0 ≤ xi ≤ 100000; 0 ≤ yi ≤ 100000).
Output:
The standard output should contain the answers for subsequent tests in the following Z lines. The result is one natural number equal to the minimum total length of the road along the streets from friends’ places of residence to the place where the meeting is to take place.
Example:
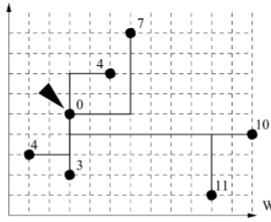
1
7
1 3
3 2
3 5
6 9
10 1
12 4
5 7
Answer: 39
Please help!!!

