FRMN - Editorial

iceknight1093 · March 26, 2025, 4:30pm

PROBLEM LINK:

Practice
Contest: Division 1
Contest: Division 2
Contest: Division 3
Contest: Division 4

Author: manasagarwal12
Tester: sushil2006
Editorialist: iceknight1093

DIFFICULTY:

Simple

PREREQUISITES:

None

PROBLEM:

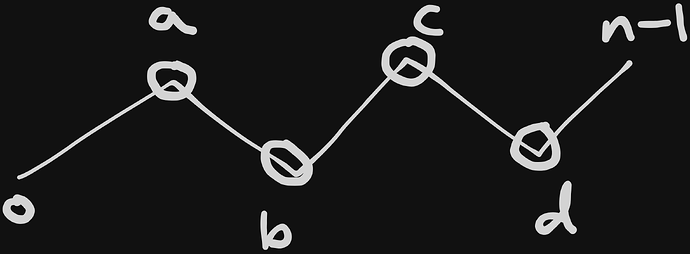
There are N mountain peaks in a line, with heights H_1, H_2, \ldots, H_N.
Adjacent peaks differ by exactly 1.

There’s one person standing at every mountain peak.
A person can move to an adjacent mountain peak, but only if it’s a height that hasn’t been visited before.

Two people are considered friends if they can meet each other at the same peak.
Find the number of friends.

EXPLANATION:

Let’s call mountain peak i a maxima if H_i \gt H_{i-1} and H_i \gt H_{i+1}.
Similarly, let’s call it a minima if it’s smaller than both neighbors.
We’ll call a peak extreme if it’s either a maxima or a minima.

Observe that because adjacent differences are equal to 1, it’s not possible for anyone to cross from one side of an extreme peak to the other side.
For example, to cross a maxima you’d have to go x \to x+1 \to x which is not allowed.

Now, let’s look at two people i and j (i \lt j).
Observe that:

If there are no extreme peaks between i and j, they can definitely meet each other (for example i can just move towards j, and will never see a repeated element).
If there’s exactly one extreme peak strictly between them (i.e. some k with i \lt k \lt j is extreme) , they can still meet, by both moving to that peak.
If there are two or more extreme peaks between them, they cannot meet at all.
This is because i cannot cross the nearest extreme peak to his right, while j cannot cross the nearest extreme peak to his left. Since these are different extremes, it’s impossible for them to ever meet.

So, two people can meet if and only if there’s at most one extreme peak strictly between them.
Now, we need to count the number of such pairs of people.

Let’s define \text{next}[i] to be the next index of an extreme peak to the right of i.
This is easy to compute:

If i+1 is extreme, then \text{next}[i] = i+1.
Otherwise, \text{next}[i] = \text{next}[i+1].

Now, suppose we fix person i, and want to count the number of people j (with j \gt i) that can be reached.
Then,

The first extreme to the right of i is at \text{next}[i].
The second extreme to the right of i is at \text{next}[\text{next}[i]].
Anyone beyond \text{next}[\text{next}[i]] cannot be reached, since there will be two extreme peaks between them.

So, the people who can be visited are exactly the range [i+1, \text{next}[\text{next}[i]]].
Simply add the length of this range to the answer for all i to obtain the overall answer.

TIME COMPLEXITY:

\mathcal{O}(N) per testcase.

CODE:

Editorialist's code (C++)

// #include <bits/allocator.h>
// #pragma GCC optimize("O3,unroll-loops")
// #pragma GCC target("avx2,bmi,bmi2,lzcnt,popcnt")
#include "bits/stdc++.h"
using namespace std;
using ll = long long int;
mt19937_64 RNG(chrono::high_resolution_clock::now().time_since_epoch().count());

int main()
{
    ios::sync_with_stdio(false); cin.tie(0);

    int t; cin >> t;
    while (t--) {
        int n; cin >> n;
        vector a(n, 0);
        for (int &x : a) cin >> x;

        vector<int> mark(n, 0), jump(n, n);
        mark[n-1] = 1;
        jump[n-1] = n;
        for (int i = n-2; i >= 0; --i) {
            if (mark[i+1]) jump[i] = i+1;
            else jump[i] = jump[i+1];
            if (i) {
                mark[i] |= a[i] > a[i-1] and a[i] > a[i+1];
                mark[i] |= a[i] < a[i-1] and a[i] < a[i+1];
            }
            else mark[i] = 1;
        }
        
        ll ans = 0;
        for (int i = 0; i < n; ++i) {
            if (jump[i] == n or jump[jump[i]] == n) ans += n - i - 1;
            else ans += jump[jump[i]] - i;
        }
        cout << ans << '\n';
    }
}

Author's code (C++)

#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll solve3(vector <ll> a,ll n){
    vector<ll>vis(n+1,0);
    vector<ll>pref(n,0);
    int j=-1;
    map<int,int>mp;
    mp[a[0]]=0;
    for(int i=1;i<n;i++){
        if(mp.find(a[i])!=mp.end()){
            j=max(j,mp[a[i]]);
            mp[a[i]]=i;
        }
        else
        mp[a[i]]=i;
        if(j!=-1)
        pref[j]++;
        
    }
  
    for(int i=n-2;i>=0;i--)
    {
        pref[i]+=pref[i+1];
    }
   
    j=n;
    mp.clear();
    mp[a[n-1]]=n-1;
    ll ans=0;

    for(int i=n-2;i>=0;i--){
        if(mp.find(a[i])!=mp.end()){
            j=min(j,mp[a[i]]);
            mp[a[i]]=i;
        }
        else 
        mp[a[i]]=i;
        if(j==n)
        {   
           // cout<<n-1-i<<endl;
            ans+=n-1-i;
        }
        else{
           
            ans+=n-1-pref[j-1]-i;
        }

    }
    return ans;

}
int main() {
    int t;
    cin>>t;
    while(t--){
        ll n;
        cin>>n;
        vector<ll> a(n);
        for(int i=0;i<n;i++)
        cin>>a[i];
        cout<<solve3(a,n)<<endl;
    }

}

Tester's code (C++)

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>

using namespace std;
using namespace __gnu_pbds;

template<typename T> using Tree = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
typedef long long int ll;
typedef long double ld;
typedef pair<int,int> pii;
typedef pair<ll,ll> pll;

#define fastio ios_base::sync_with_stdio(false); cin.tie(NULL)
#define pb push_back
#define endl '\n'
#define sz(a) (int)a.size()
#define setbits(x) __builtin_popcountll(x)
#define ff first
#define ss second
#define conts continue
#define ceil2(x,y) ((x+y-1)/(y))
#define all(a) a.begin(), a.end()
#define rall(a) a.rbegin(), a.rend()
#define yes cout << "Yes" << endl
#define no cout << "No" << endl

#define rep(i,n) for(int i = 0; i < n; ++i)
#define rep1(i,n) for(int i = 1; i <= n; ++i)
#define rev(i,s,e) for(int i = s; i >= e; --i)
#define trav(i,a) for(auto &i : a)

template<typename T>
void amin(T &a, T b) {
    a = min(a,b);
}

template<typename T>
void amax(T &a, T b) {
    a = max(a,b);
}

#ifdef LOCAL
#include "debug.h"
#else
#define debug(...) 42
#endif

/*



*/

const int MOD = 1e9 + 7;
const int N = 1e5 + 5;
const int inf1 = int(1e9) + 5;
const ll inf2 = ll(1e18) + 5;

void solve(int test_case){
    ll n; cin >> n;
    vector<ll> a(n+5);
    rep1(i,n) cin >> a[i];
    vector<ll> b(n+5);
    rep1(i,n) b[i] = a[i] < a[i+1];
    b[n] = -1;
    vector<ll> nxt(n+5,n);

    rev(i,n-1,1){
        if(b[i] == b[i+1]) nxt[i] = nxt[i+1];
        else nxt[i] = i;
    }

    ll ans = 0;

    rep1(i,n-1){
        ll j = i-1;
        rep1(iter,2){
            j++;
            j = nxt[j];
        }
        amin(j,n-1);
        ans += j-i+1;
    }

    cout << ans << endl;
}

int main()
{
    fastio;

    int t = 1;
    cin >> t;

    rep1(i, t) {
        solve(i);
    }

    return 0;
}

firstexception · March 26, 2025, 4:47pm

MY solution for it: (using the fact abs(h[i]-h[i+1])=1)

for each i precompute the immediate longest decreasing or increasing lengths ( because of this abs(h[i]-h[i+1])=1 ) in the prefix and suffix
then you get a range till which h[i] can reach while satisfying the constraints
finally for each i do the binary search to find out how many range intersect with the ith range on the right hand side of i ([i+1,n])
then, Sum all of them for all i

why longest increasing or decreasing ?
because each next element of h[i] will be either previous +1 or +0 (because of the above fact)
if it +0 that means, we have founded a repeated value for some element between h[i] and till now
if it +1 that means , we can take it, because for sure it will be distinct (try some cases on pen and paper)

grecil · March 26, 2025, 5:01pm

Here is my idea. I will find all peaks and crests and store them in an array. I will pad the array with 0 in front and n-1 in back. We know that all elements around peak/crest can always meet at peak/crest. Let sm(x) = (x*x+x)/2 (the number of friendships between x people).

We will initialise the ans variable and add the all sm(arr[i+1]-arr[i-1]+1) to it, which is essentially all friendships between index 0 to b, a to c, c to n-1.

Some friendships have been counted twice. So we will reduce them from the answer. We will reduce all sm(arr[i+1]-arr[i]) from ans. We reduce friendships between a to b, b to c, c to d from ans.

grecil · March 26, 2025, 6:54pm

sm(x) is (x*x-x)/2

scorch_earth · March 27, 2025, 4:14am

This is what i did aswell

dheeeraj_001 · March 27, 2025, 4:26am

x(x-1)/2 or xc2 (Same)

dheeeraj_001 · March 27, 2025, 5:31am

Here is implementation , one edge case to handle , when there is no peak/crest.

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef vector<ll> vll;

void solve() {
    int n;
    cin >> n;
    vll v(n);
    
    for (ll i = 0; i < n; i++)
        cin >> v[i];

    vector<int> vv;
    if (n == 1) {
        cout << 0 << endl;
        return;
    }

    vv.push_back(0);
    for (int i = 1; i < n - 1; i++) {
        if ((v[i] > v[i - 1] && v[i] > v[i + 1]) || 
            (v[i] < v[i - 1] && v[i] < v[i + 1])) {
            vv.push_back(i);
        }
    }

    vv.push_back(n - 1);
    ll ans = 0;
    int m = vv.size();
    
    if (vv.size() == 2) {
        int pp = vv[m - 1] - vv[0] + 1;
        ans += (1LL * pp * (pp - 1)) / 2;
        cout << ans << endl;
        return;
    }

    for (int i = 1; i < m - 1; i++) {
        int pp = (vv[i + 1] - vv[i - 1] + 1);
        ans += (1LL * pp * (pp - 1)) / 2;
    }

    for (int i = 1; i < m - 2; i++) {
        int pp = (vv[i + 1] - vv[i] + 1);
        ans -= (1LL * pp * (pp - 1)) / 2;
    }

    cout << ans << endl;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int t, n;
    cin >> t;
    while (t--) {
        solve();
    }

    return 0;
}

grecil · March 27, 2025, 6:23am

I got one wrong submission because of this. Fixed it and got AC.

shiveshkaushik · March 27, 2025, 3:55pm

but how can you precompute in linear time complexity? because for every element we have to search its left and right then it would O(N2) for precomputation.