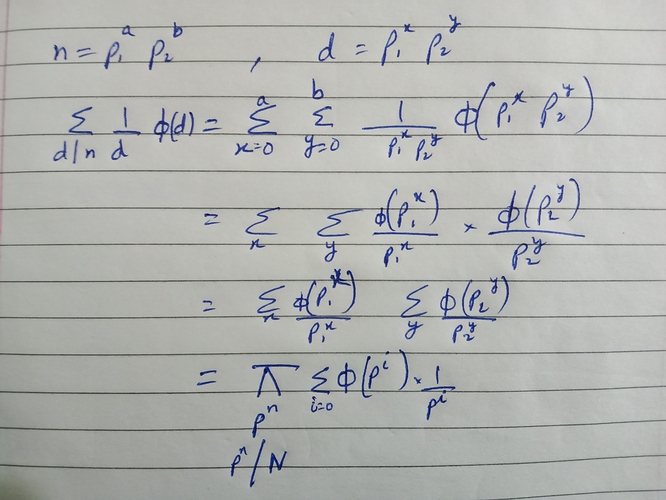PROBLEM LINK: Rick in Space
AUTHOR: panik
DIFFICULTY: Medium
PREREQUISITES: Maths, Totient function

Let’s denote the totient function as T ( N ). So as we know totient function tells
us the count of no.s less than N which are coprime with N. Lets not get in to
the proof of that as it is easily available on the internet. Now what we need to find
out in the question is the count of no.s having GCD with N = d for all possible d,
where d is the divisor of N, as GCD won’t give any other output apart from this.
For a specific GCD count of no.s giving such GCD will be d * T ( N/d )
Therefore the sum of GCD for all no.s less than equal to N is sum ( d * T ( N / d) )
This can also be converted to N/d * T ( d ) ( let N/d = x, now even x is also a
divisor, and hence we can convert it to this form)
Now just try to understand the above proof to find the sum of GCD( x ,N ) for x
from 1 to N.
In the proof, p denotes prime no. and n denotes the power of prime no. in N.
Once you understand the core logic the only thing left to find out is the prime
factors and their frequency in N. Now this step requires some optimizations
due to the given constraints. For this we use a very famous trick sieves of
Eratosthenes.
Using this we pre-calculate all the prime no. upto 10^6. Now the question
arises that if N contains a prime no. greater than 10^6. For this, you need to
understand that N can contain at most 1 prime no. greater than 10^6 and that
with a power of 1 at max. Because if it contains more than 1 prime no. greater
than 10^6, it would exceed the given constraints. Using this we find the prime
factors and their powers in N. A no. <10^12 can have at most 12/13 distinct
prime factors as it roots, so the answer to the question using the above-derived formula will only take O( distinct divisors ) in implementation which is
practically just a constant time.
To read more about totient function :
Expected solution: here