PROBLEM LINK:
Contest Division 1
Contest Division 2
Contest Division 3
Practice
Setter: Daanish Mahajan
Tester: Istvan Nagy
Editorialist: Taranpreet Singh
DIFFICULTY
Easy-Medium
PREREQUISITES
Geometry, Trigonometry, Shoelace Formula
PROBLEM
Given a convex polygon with N sides, answer Q queries, where each query is described by integers (v_i, t_i) such that all sides of polygon start moving parallel to their respective perpendicular vector away from the centroid with velocity v_i for t_i seconds, then find the area of the newly formed polygon.
Queries are independent of each other.
QUICK EXPLANATION
- Divide the newly formed polygon into three categories of regions, one being the original polygon, the other being the region of the rectangles formed by sides of the original polygon, and the last region being the symmetric triangles formed at each vertex.
- Compute the area of a given polygon using the shoelace formula and the area of the second type region by computing the sum of the length of sides of the given polygon.
- The area of the third region can be computed by a bit of trigonometry, by drawing perpendicular from vertices to sides of the newly formed polygon.
EXPLANATION
Let’s consider an example first

Assume that polygon ABC is the given polygon, and polygon DEF is the polygon formed after the operation is applied, moving each side of polygon d = v_i * t_i units away.
Note that |AL| = |BK| = |BJ| = |CI| = |CH| = |AG| = d and AG \perp AC, CH \perp AC, CI \perp BC, BJ \perp BC, KB \perp AB and AL \perp AB.
We can divide polygon DEF into regions of the following three categories.
- Polygon ABC
- Regions sharing a side with polygon ABC (Regions ABKL, BCIJ, and ACHG)
- Regions only sharing a corner with vertices of ABC (Regions DGA, DLA, EKB, ELB, FHC, FIC)
Region 1
The area of polygon ABC can be computed before all queries using the shoelace formula, or any other formula.
Region 2
These regions are the rectangles formed sharing one side with the original polygon. Regions ABKL, BCIJ, and ACHG are the regions of this type. Since all these are rectangles, the area is length times the breadth.
For region ABDL, the area is |AB|*|AL| = |AB| * d.
For region BCIJ, the area is |BC|*|BJ| = |BC| * d.
For region ACHG, the area is |AC|*|AG| = |AC| * d.
Hence, the total area of all regions of this type is given by d * (|AB| + |BC| + |CA|) which is equal to d times perimeter of the given polygon.
Hence, if we have computed the perimeter of the given polygon beforehand, we can compute the area of all regions of the second category in O(1)
Region 3
Regions DGA, DLA, EKB, EJB, FHC, FIC are the regions in this category, which are all triangles. Moreover, DGA and DLA are symmetric, EJB and EKB are symmetric, and FHC and FIC are symmetric. We want to compute the sum of areas of these regions.
Considering triangle DGA first, we know that GA \perp DG, so this is a right-angled triangle. We also have AC \parallel DF. We also know that DM is the angle bisector of \angle BAC. Let’s assume \angle BAC = \alpha, so \angle MAC = \alpha /2. Since AC \parallel DF, we have \angle ADG = \alpha /2.
We also have |AG| = d. The area of this triangle is given by base * height /2, which is |AG| * |DG| /2 = \frac{d * d * cot(\alpha /2)}{2}
Since DGA and DLA are symmetric, the area of the region DLAG is d^2 * cot(\angle BAC /2). Similarly, we can prove area of region EKBJ as d^2 * cot(\angle ABC /2) and the area of region FHCI as d^2 * cot(\angle ACB /2)
So, the sum of area of regions of this category can be written as d^2 * \displaystyle \sum_{i = 1}^N \cot \left(\frac{\angle V_{i-1} V_i V_{i+1}}{2} \right).
Once again, we can compute \displaystyle \sum_{i = 1}^N \cot \left(\frac{\angle V_{i-1} V_i V_{i+1}}{2} \right) before answering queries.
Lastly, angle between three points can be calculated using cosine rule. Specifically, \angle BAC is given by \displaystyle cos^{-1}\left(\frac{|AB|^2+|AC|^2-|BC|^2}{2*|AB|*|AC|}\right).
Summarizing
Let’s compute X being area of given polygon, S being perimeter of given polygon, and Z = \displaystyle \sum_{i = 1}^N \cot \left(\frac{\angle V_{i-1} V_i V_{i+1}}{2} \right).
The final area is given by formula X + S*d + Z *d*d.
TIME COMPLEXITY
The time complexity is O(N+Q) per test case.
SOLUTIONS
Setter's Solution
# include<bits/stdc++.h>
# define pb push_back
# define pii pair<int, int>
# define mp make_pair
# define ll long long int
# define pll pair<ll, ll>
# define ld long double
# define pld pair<ld, ld>
using namespace std;
FILE *fp;
ofstream outfile;
const string newln = "\n", space = " ";
const int maxvt = 1e5, minc = 0, maxc = 2e6, maxtn = 5e5, maxtq = 5e5, maxn = 1e4, maxq = 1e4, maxt = 1e2;
ll xc[maxn], yc[maxn];
pll vec(int p1, int p2){
return {xc[p1] - xc[p2], yc[p1] - yc[p2]};
}
ll cp(pll p1, pll p2){
return p1.first * p2.second - p1.second * p2.first;
}
ll dp(pll p1, pll p2){
return p1.first * p2.first + p1.second * p2.second;
}
ld vlen(pll p){
return sqrt(p.first * p.first + p.second * p.second);
}
bool ang(int x, int n){
pll p1 = vec((x + 1) % n, x), p2 = vec((x - 1 + n) % n, x);
ll cross = cp(p1, p2), dot = dp(p1, p2);
// cout << cross << " " << dot << endl;
return cross > dot * tan(M_PI / 180);
}
ld hang(int x, int n){
pll p1 = vec((x + 1) % n, x), p2 = vec((x - 1 + n) % n, x);
ll dot = dp(p1, p2);
ld mul = vlen(p1) * vlen(p2);
return sqrt((mul + dot) / (mul - dot));
}
int main()
{
// for(int test = 1; test <= 1; test++){
// string in = "/home/daanish/CP/codechef/LearningTeam/Problems/geo1/in" + to_string(test) + ".in";
// string out = "/home/daanish/CP/codechef/LearningTeam/Problems/geo1/out" + to_string(test) + ".out";
// freopen(in.c_str(), "r", stdin);
// freopen(out.c_str(), "w", stdout);
ios_base::sync_with_stdio(false); cin.tie(NULL);
int t, n, q, v, tt; cin >> t;
int sumn = 0, sumq = 0;
ld mans = 0;
while(t--){
cin >> n >> q; sumn += n; sumq += q;
for(int i = 0; i < n; i++){
cin >> xc[i] >> yc[i];
}
for(int i = 0; i < n; i++){
assert(ang(i, n));
}
ld area = 0;
for(int i = 0; i < n; i++){
area += (xc[i] * yc[(i + 1) % n] - yc[i] * xc[(i + 1) % n]);
}
area = abs(area) / 2;
ld hfang = 0, len = 0;
for(int i = 0; i < n; i++){
hfang += hang(i, n);
len += vlen(vec(i, (i + 1) % n));
}
// cout << area << " " << hfang << " " << len << endl;
for(int i = 0; i < q; i++){
cin >> v >> tt;
ll vt = v * tt;
ld ans = vt * (len + vt * hfang) + area;
mans = max(mans, ans);
printf("%.9Lf\n", ans);
}
}
// cout << mans << endl;
assert(sumn <= maxtn); assert(sumq <= maxtq);
// }
}
Tester's Solution
#include <iostream>
#include <cassert>
#include <vector>
#include <set>
#include <map>
#include <algorithm>
#include <random>
#ifdef HOME
#include <windows.h>
#endif
#define all(x) (x).begin(), (x).end()
#define rall(x) (x).rbegin(), (x).rend()
#define forn(i, n) for (int i = 0; i < (int)(n); ++i)
#define for1(i, n) for (int i = 1; i <= (int)(n); ++i)
#define ford(i, n) for (int i = (int)(n) - 1; i >= 0; --i)
#define fore(i, a, b) for (int i = (int)(a); i <= (int)(b); ++i)
template<class T> bool umin(T &a, T b) { return a > b ? (a = b, true) : false; }
template<class T> bool umax(T &a, T b) { return a < b ? (a = b, true) : false; }
using namespace std;
struct point2d {
long double x, y;
point2d() {}
point2d(long double x, long double y) : x(x), y(y) {}
point2d& operator+=(const point2d& t) {
x += t.x;
y += t.y;
return *this;
}
point2d& operator-=(const point2d& t) {
x -= t.x;
y -= t.y;
return *this;
}
point2d& operator*=(long double t) {
x *= t;
y *= t;
return *this;
}
point2d& operator/=(long double t) {
x /= t;
y /= t;
return *this;
}
point2d operator+(const point2d& t) const {
return point2d(*this) += t;
}
point2d operator-(const point2d& t) const {
return point2d(*this) -= t;
}
point2d operator*(long double t) const {
return point2d(*this) *= t;
}
point2d operator/(long double t) const {
return point2d(*this) /= t;
}
};
point2d operator*(long double a, point2d b) {
return b * a;
}
long double area(const vector<point2d>& fig) {
long double res = 0;
for (unsigned i = 0; i < fig.size(); i++) {
point2d p = i ? fig[i - 1] : fig.back();
point2d q = fig[i];
res += (p.x - q.x) * (p.y + q.y);
}
return fabs(res) / 2;
}
long double dot(point2d a, point2d b) {
return a.x * b.x + a.y * b.y;
}
long double norm(point2d a) {
return dot(a, a);
}
long double abs(point2d a) {
return sqrt(norm(a));
}
long double angle(point2d a, point2d b) {
return acos(dot(a, b) / abs(a) / abs(b));
}
long double getAngleCos(point2d a, point2d b) {
return dot(a, b) / abs(a) / abs(b);
}
long double getAngleHalfTanFromCos(long double cosAngle) {
return sqrt((1 - cosAngle) / (1 + cosAngle));
}
int main(int argc, char** argv)
{
#ifdef HOME
if(IsDebuggerPresent())
{
freopen("../in.txt", "rb", stdin);
freopen("../out.txt", "wb", stdout);
}
#endif
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.precision(10);
cout << fixed;
int T;
cin >> T;
const long double pi = acos(0);
forn(tc, T)
{
uint32_t N, Q;
cin >> N >> Q;
vector<point2d> V(N);
for (auto& p : V)
{
uint32_t xx, yy;
cin >> xx >> yy;
p.x = xx;
p.y = yy;
}
long double ar = area(V);
long double sidelen = 0;
long double anglelen = 0;
forn(i, N)
{
point2d currSide = V[i] - V[(i + 1) % N];
sidelen += abs(currSide);
}
forn(i, N)
{
point2d currSide = V[i] - V[(i + 1) % N];
point2d nextSide = V[(i + 1) % N] - V[(i + 2) % N];
long double cosAngle = getAngleCos(currSide, nextSide);
long double currTriangleArea2 = getAngleHalfTanFromCos(cosAngle);
// long double currAngle = angle(currSide, nextSide);
// long double currTriangleArea = tan((currAngle/2));
anglelen += currTriangleArea2;
}
forn(q, Q)
{
long double v, t;
cin >> v >> t;
long double d = v * t;
long double res = ar + (sidelen + anglelen * d) * d;
printf("%.9Lf\n", res);
}
}
return 0;
}
Editorialist's Solution
import java.util.*;
import java.io.*;
import java.text.DecimalFormat;
class GEO1{
//SOLUTION BEGIN
void pre() throws Exception{}
void solve(int TC) throws Exception{
int N = ni(), Q = ni();
double[][] P = new double[N][];
double cotTheta = 0, side = 0, init = 0;
for(int i = 0; i< N; i++)
P[i] = new double[]{nd(), nd()};
for(int i = 0; i< N; i++){
int i1 = (i+N-1)%N, i2 = (i+1)%N;
double a = dist(P[i], P[i1]), b = dist(P[i], P[i2]), c = dist(P[i1], P[i2]);
double ang = Math.acos((a*a+b*b-c*c)/(2*a*b))/2;
cotTheta += 1/Math.tan(ang);
side += a;
init += P[i][0]*P[i2][1]-P[i][1]*P[i2][0];
}
init /= 2;
DecimalFormat df = new DecimalFormat("0.00000000");
for(int q = 0; q< Q; q++){
double ti = nl()*nl();
double area = init + side*ti + cotTheta*ti*ti;
pn(df.format(area));
}
}
double dist(double[] p1, double[] p2){
return Math.sqrt((p1[0]-p2[0])*(p1[0]-p2[0]) + (p1[1]-p2[1])*(p1[1]-p2[1]));
}
double area(double[] p1, double[] p2, double[] p3){
return 0.5*(p1[0]*(p2[1]-p3[1]) + p2[0]*(p3[1]-p1[1])+p3[0]*(p1[1]-p2[1]));
}
//SOLUTION END
void hold(boolean b)throws Exception{if(!b)throw new Exception("Hold right there, Sparky!");}
static boolean multipleTC = true;
FastReader in;PrintWriter out;
void run() throws Exception{
in = new FastReader();
out = new PrintWriter(System.out);
//Solution Credits: Taranpreet Singh
int T = (multipleTC)?ni():1;
pre();for(int t = 1; t<= T; t++)solve(t);
out.flush();
out.close();
}
public static void main(String[] args) throws Exception{
new GEO1().run();
}
int bit(long n){return (n==0)?0:(1+bit(n&(n-1)));}
void p(Object o){out.print(o);}
void pn(Object o){out.println(o);}
void pni(Object o){out.println(o);out.flush();}
String n()throws Exception{return in.next();}
String nln()throws Exception{return in.nextLine();}
int ni()throws Exception{return Integer.parseInt(in.next());}
long nl()throws Exception{return Long.parseLong(in.next());}
double nd()throws Exception{return Double.parseDouble(in.next());}
class FastReader{
BufferedReader br;
StringTokenizer st;
public FastReader(){
br = new BufferedReader(new InputStreamReader(System.in));
}
public FastReader(String s) throws Exception{
br = new BufferedReader(new FileReader(s));
}
String next() throws Exception{
while (st == null || !st.hasMoreElements()){
try{
st = new StringTokenizer(br.readLine());
}catch (IOException e){
throw new Exception(e.toString());
}
}
return st.nextToken();
}
String nextLine() throws Exception{
String str = "";
try{
str = br.readLine();
}catch (IOException e){
throw new Exception(e.toString());
}
return str;
}
}
}
Feel free to share your approach. Suggestions are welcomed as always. ![]()
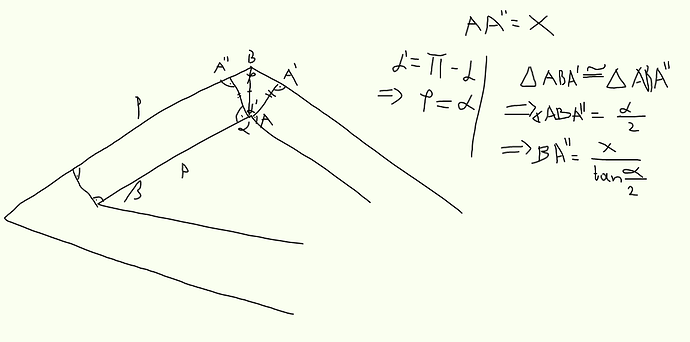
 it won’t work I don’t know the reason, I thought this was the property of two similar polygons.
it won’t work I don’t know the reason, I thought this was the property of two similar polygons. . i hope this makes sense.
. i hope this makes sense.
