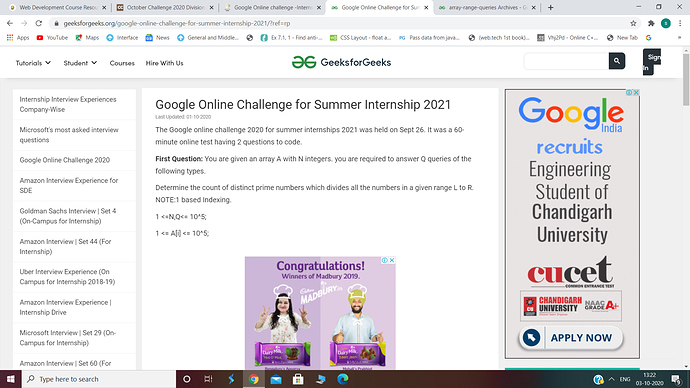
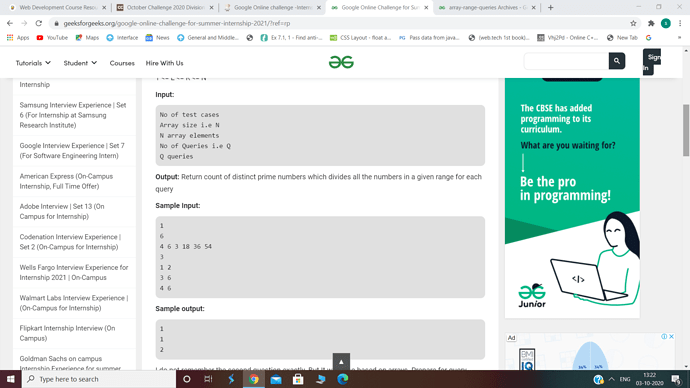
The answer for each query would be the number of prime factors of GCD( A[l], A[l+1]… A[R])
So you can split each query into 2 subtasks :
-
Find the GCD of the range L to R. → This can be achieved in O(log^2(n) ) using a sparse table. SPARSE TABLE
-
Calculate the number of distinct prime factors → This can be achieved in O(log(n)) by storing the Smallest Prime factor … or even O(1) by precomputing using Sieve.
SIEVE
So the overall T.C for each query would be O(log^3(n)).
What I would have tried would be something like this:
Before the queries, simplify the numbers. In the sense, first find the prime factors of the numbers, and then initialize the number as the product of the prime factors
Eg
12 = 2 * 2 * 3
I would initialize it to 6 = (2 * 3)
Now, as a[i] <=10^5, the new number will have at most 10 prime factors. (The product of the lowest 10 prime numbers are > 10^5), so keep a vector of each element, and store the prime factors of the element in that vector.
Now, create a segment tree.
Suppose node i has a range from l to r, it will store the count of distinct prime factors from l to r and the prime factors which are there.
Since, we will merge two vectors (the one consisting of prime factors) into one (the vectors of two children into the parent vector) in a segment tree, it will take at most 2 * (MaxSizeVector + MaxSizeVector) = 40 using set_intersection()
The number of times we are doing this is N times => 10^5 *40 => 4 * 10^6, which is well within our time limit. (Note: we are not merging the vectors of the children, as that has already been formed before)
Now, for each query, query into the segment tree the same way, and you will have the answer.
Complexity = O(Q * 40 * log(n)), which is more or less equal to O(Q * log(3n)) for high N values.