PROBLEM LINK:
Author: Arthur Nascimento
Tester: Felipe Mota
Editorialist: Rajarshi Basu
DIFFICULTY:
Medium
PREREQUISITES:
Binary-Search, Adhoc
PROBLEM:
We have to guess a number N, 1 \leq N \leq 10^9. We can query an adaptive judge, with a value X, and it can tell us whether X > N ( when it will return G), X < N ( when it will return L) or X=N. However, it can also lie: it can return X > N when X<N, or X<N when actually X>N. Note that it won’t lie about equality. Further, it cannot lie twice in a row. Guess the value of N in at most 120 queries.
EXPLANATION:
This problem is not based much on finding observations and building upon them. It is much more adhoc. Hence, I’ll write this as a sequence of what one could have done while solving this problem, and not as a sequence of Observations. That said, let’s move ahead:
Some Preliminary Thinking
The problem seems very close to binary-search, but it isn’t clear how we can proceed since the judge can lie as well. Making multiple queries at the same location also doesn’t reveal any useful information, since we don’t know which is truth and which is a lie. Nor can we take help of any randomisation tactics since the judge is adaptive.
Maybe Brute?
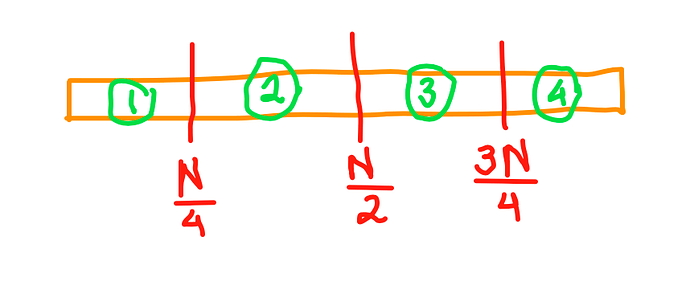
We might think that since just querying a bunch of times at the middle point doesn’t help, maybe we can query at a bunch of places in some sequence. To me, it felt appropriate to query at points \{\frac{N}{2}, \frac{N}{4} ,\frac{3N}{4}\}. In what order, how many times? Well, I fixed a point as the hidden value (since that shouldn’t matter for our testing). Then, I brute-forced the length and the order of queries, as well as which is a lie and which is a truth. This means every query would have given a plausible set of regions (here regions are 1,2,3,4, which are separated by our set of query points), and my goal was to see if, in any order of queries, a particular region could always be found as common, irrespective of which were lies and which were the truth. Turned out, the intersection was always null. sad sad crie crie
THE ZONES:
Key takeaway from the above bruteforcing?
Well, it seemed unlikely after this that we can use some queries and fixate a particular region as our plausible zone. Thus, maybe instead of trying to fixate on a particular region, what if a better way was to eliminate the zones?
What next?
Trying to eliminate
Well, again, taking the three query points of \{\frac{N}{4}, \frac{N}{2}, \frac{3N}{4} \} seems like a reasonable choice. Now, let’s query at \frac{N}{2}, and WLOG assume that we got G back from the judge. Then, let’s query at \frac{N}{4}. What happens now?
More Explanation
If we again get back G, then we definitely know that region 1 can definitely be eliminated. However, if we get back L, then we definitely know that region 2 can be eliminated! N0ice.
We can argue similarly if we had got L after querying at \frac{N}{2}, and would have queried at \frac{3N}{4} after it.
How does that help?
Well, now we are effectively removing \frac{1}{4} of the search space for every 2 queries that we make. This solution is intended to give up to 75pnts. (Find out the exact number of queries required!)
Let's go for 100 points!
We have to slightly (read: a lot) modify our solution. It isn’t obvious how we can reduce more than 25\%.
How much to we reduce by?
Try to reduce by 33\% for every 2 queries.
Hint 1:
Instead of trying to use exactly 2 new queries for each 33\% reduction, maybe we can do something trickier?
Hint 2:
We still need to query at \frac{N}{2}.
Hint 3:
Try to split it into uneven pieces
Full Solution
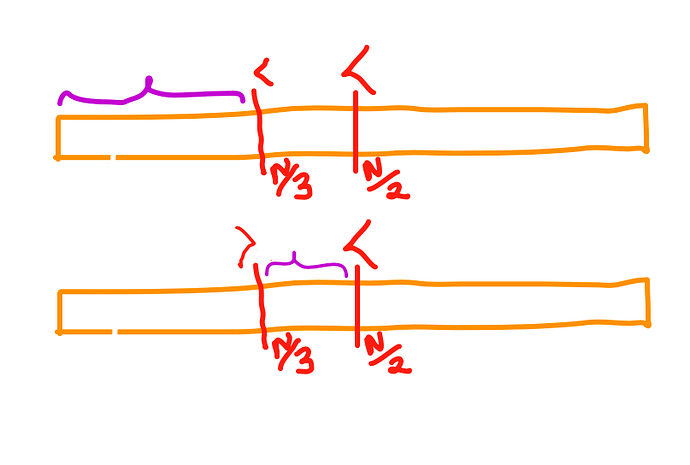
Let’s say we got G at \frac{N}{2}. Now, consider the portion 1 to \frac{N}{2}-1. Now, query at \frac{N}{3}. If, we get a G, that means 1 to \frac{N}{3} is definitely eliminated. Otherwise, \frac{N}{3} to \frac{N}{2} definitely gets eliminated. But hold on \dots doesn’t that mean that in the worst case we are just eliminating a total length of \frac{N}{6} in the worst case \dots using 2 queries? Well yes but no. The trick is, this last query (ie, at \frac{N}{3}) is pretty close to the centre of the sequence after we have eliminated \frac{N}{3} to \frac{N}{2}. Hence, we can just use its result as the first query in the next iteration!
This solution should give full points. See Tester’s code for more details.
Dry Run
Let’s go through an example:
- Let’s say our initial range of number’s were [1 \dots 100]
- First, we query at 50, and let’s assume we got G
- Now, let’s say we query at 33, and we get G. Then we just remove [1 \dots 33], and again start over, since we have removed 33% using 2 queries.
- Let’s look at the other case, where we get L. Then, we delete [33 \dots 50].
- Now, our range is [1 \dots 32] \cup [51 \dots 100], and we had got a L at 33. Hence, we query at 66. If we get a L, our range reduces to [1 \dots 33] \cup [51 \dots 65], and we can start over.
- Else, our range becomes [1 \dots 33] \cup [67 \dots 100], and our last result is a G at 66.
- We continue this process, until we get to remove a 33\%, or hit the actual answer. Once we remove a 33\%, we start over, discarding our previous query answer.
Complexity Analysis
We can show the following:
- If the process takes an odd amount X of turns, the remaining available numbers will be something like \frac{1}{2} * \frac{2}{3}^{\frac{X - 3}{ 2}}
- If the process takes an even amount Y of turns, the remaining available numbers will be something like \frac{2}{3}^{\frac{Y}{2}}
So we could do some round-ups and say that we remove ~(1 - \sqrt{\frac{2}{3}}) (to handle the \frac{1}{2}) per operation, which leads to removing ~33\% per 2 queries.
QUICK REMINDERS:
Remind Me
Since we are eliminating, all the plausible values are not in a contiguous range. We can maintain them as a list of valid ranges. Again, See setter’s code for more details.
Oh, and don’t forget to flush the output!
SOLUTIONS:
Tester's Code
#include <bits/stdc++.h>
using namespace std;
int main(){
int n;
cin >> n;
vector<pair<int,int>> ranges, nxt_ranges;
ranges.push_back({1, n});
auto size = [&](){
int len = 0;
for(auto e : ranges) len += e.second - e.first + 1;
return len;
};
int cnt_q = 0;
auto query = [&](int x){
cnt_q++;
assert(cnt_q <= 100);
cout << x << endl;
char ans;
cin >> ans;
if(ans == 'E'){
exit(0);
}
return ans;
};
auto kth = [&](int k){
for(auto e : ranges){
int len = e.second - e.first + 1;
if(k > len)
k -= len;
else
return e.first + k - 1;
}
return -1;
};
auto count_small = [&](int x){
int ans = 0;
for(auto e : ranges){
if(e.second <= x){
ans += e.second - e.first + 1;
} else {
if(x >= e.first) ans += x - e.first + 1;
}
}
return ans;
};
auto remove = [&](int l, int r){
nxt_ranges.clear();
for(auto e : ranges){
if(e.second < l) nxt_ranges.push_back(e);
else if(e.first > r) nxt_ranges.push_back(e);
else {
if(e.first < l) nxt_ranges.push_back({e.first, l - 1});
if(e.second > r) nxt_ranges.push_back({r + 1, e.second});
}
}
ranges = nxt_ranges;
};
while(true){
int len = size();
if (len <= 5){
for(int i = 1; i <= len; i++){
query(kth(i));
}
break;
}
int x = kth(len / 2);
char last = query(x);
int L = len / 2 - 1, R = len - len / 2;
int qr[2] = {x, x};
bool done = false;
for(int i = 0; L > 1 && R > 1 && !done;){
double delta = 0.33;
if(last == 'G'){
int np = kth(L * (1 - delta));
char nxt = query(np);
if(nxt == last){
remove(1, np);
remove(qr[0], qr[1]);
done = true;
} else {
qr[0] = qr[1];
qr[1] = np;
}
last = nxt;
L = count_small(np - 1);
} else {
int np = kth(len - R * (1 - delta));
char nxt = query(np);
if(nxt == last){
remove(np, n);
remove(qr[1], qr[0]);
done = true;
} else {
qr[0] = qr[1];
qr[1] = np;
}
last = nxt;
R = len - count_small(np);
}
if(!done){
remove(min(qr[0], qr[1]), max(qr[0], qr[1]));
len = size();
L = count_small(min(qr[0], qr[1]));
R = len - count_small(max(qr[0], qr[1]));
}
}
}
assert(0);
return 0;
}
Please give me suggestions if anything is unclear so that I can improve. Thanks ![]()