i am trying to solve this problem but not getting idea could you guys help please
problem : CodeChef: Practical coding for everyone
Let’s look at a standard trick that shows up very often in matrix problems.
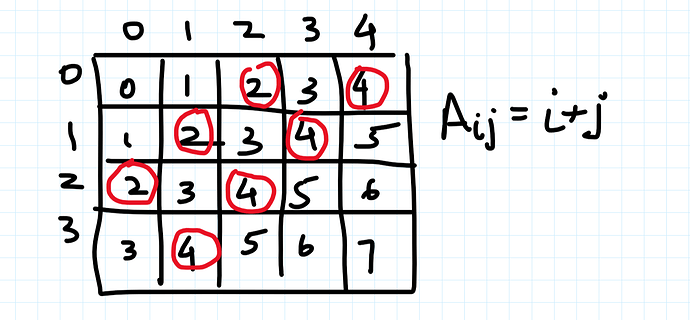
Now it’s pretty clear that i+j remains invariant for all the cells within a single diagonal parallel to the main diagonal.
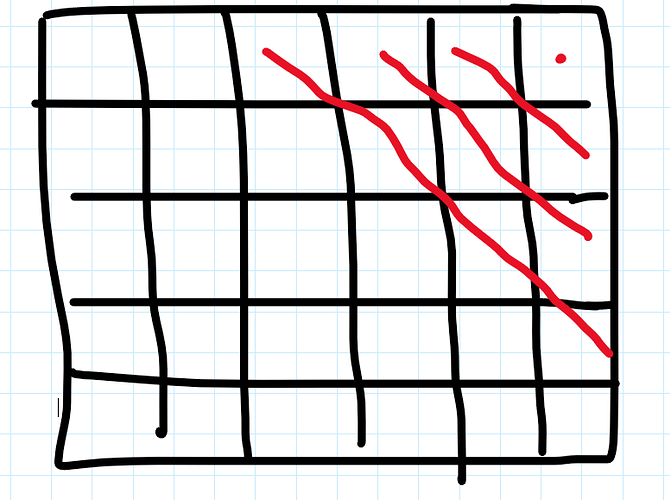
So we’ll divide the cells into various disjoint classes where each class represents a diagonal as shown in the figure:
D_k represents set of all cells of the diagonal k.( Set of all cells (i,j) for which i+j=k)
D'_k represents the same for the secondary diagonals.
Coming back to the problem there’s only one key observation that one needs to make which is as follows.
Any path starting from cell (0,0) and terminating at any cell (r,c) will be of length (r+c) and will have exactly one cell from D_i \forall i=0,1...(r+c)
Now the problem is pretty trivial and boils down to making all cells in D_i either black or white and the same holds for the secondary diagonals. Note that you’ve to make both D_i and D'_i of the same color. Rest is just trivial greedy details of which leave for you to figure out.
AC_CODE
#include "bits/stdc++.h"
using namespace std ;
void solve(){
int n,m,k ;
cin >> n>>m >>k ;
vector<string>a(m) ;
for(string &x:a)
cin >> x ;
int N = k-1+n,ans=0;
vector<int>b(N+1),w(N+1) ;
auto get=[&](){
for(int i=0;i<k;i++)
for(int j=0;j<n+1;j++)
b[i+j]+=(a[i][j]=='B'),w[i+j]+=(a[i][j]=='W') ;
} ;
get() ;
for(string &x:a)
reverse(x.begin(),x.end());
get() ;
for(int i=0;i<k;i++)
b[i+n]-=(a[i][n]=='B'),w[i+n]-=(a[i][n]=='W') ;
for(int i=0;i<N;i++)
ans+=min(b[i],w[i]) ;
cout << ans << '\n' ;
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int TC ;
cin >>TC ;
while(TC--)
solve() ;
}