Here’s an Atcoder Problem on graph. Most people had solved it using union-find algorithm which I’m unable to understand. But on codeforces discussion, I saw that this question can also be solved using DFS/BFS.
Can anyone explain, how can I solve it using DFS and BFS. I’m stuck at it since morning. Help!
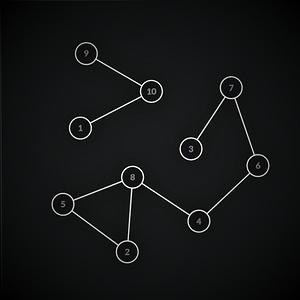
You can treat the given network as a graph such that any 2 nodes sharing a friendship relation will be connected by an edge now in order to find the number of friend candidates for each user what you can do is to find the size of the fully connected component which contains a given node and then subtract all the friendship & blockship relations of that particular node which are also present in the same connected component. For example, consider the sample given in the problem
INPUT
10 9 3
10 1
6 7
8 2
2 5
8 4
7 3
10 9
6 4
5 8
2 6
7 5
3 1
OUTPUT:1 3 5 4 3 3 3 3 1 0
/*
_ __ _ _____ _____ _____
___ _ _| |__ ___ / _|_ __ ___ __ _| | __ |___ |___ |___ |
/ __| | | | '_ \ / _ \ |_| '__/ _ \/ _` | |/ / / / / / / /
| (__| |_| | |_) | __/ _| | | __/ (_| | < / / / / / /
\___|\__,_|_.__/ \___|_| |_| \___|\__,_|_|\_\ /_/ /_/ /_/
*/
#include<bits/stdc++.h>
using namespace std;
typedef long long ll ;
typedef pair<int,int> pii;
typedef pair<ll,ll> pll;
typedef vector<ll> vi;
typedef vector<pll> vpll;
typedef unordered_map <ll,ll> umap ;
//#pragma GCC optimize "trapv"
#define loop(i,a,b) for(ll i=a ;i<b;i++)
#define For(i,n) for(int i=0;i<(ll)n;i++)
#define Rev(i,n) for(int i=n-1;i>=0;i--)
#define Rep(i,n) for(int i=1;i<=n;++i)
#define F first
#define S second
#define pb push_back
#define em emplace_back
#define all(v) (v).begin(),(v).end()
#define mems(x, y) memset(x, y, sizeof(x))
#define sz(v) (v).size()
#define mp(a,b) make_pair(a,b)
#define pf(n) cout<<n<<"\n"
#define pff(n) cout << n << " " ;
long const M=1e9+7;
const long mxN =1e5+2 ;
const long mxNN =1e6+2 ;
int n,m,k,a,b,ans[mxN];// declarations ans[i] stores the ans for ith user
unordered_set<int>component ;// unordered set to store all the nodes of current component of analysis
bool visited[mxN] ;// boolean array to keep track of all visited nodes
vi friendship[mxN],blockship[mxN] ;//adjacency matrices storing all friendship nd blockship relations
// the following dfs returns the size of connected component in which th source is also it stores all the nodes of that component in unordered set
int dfs(int v){
int ans =1 ;// initialise for each node ans as 1 (node itself)
visited[v]=true ;component.insert(v) ;
for(int x :friendship[v])// for each adjacent node check if it is not visited yet then add its contribution
if(!visited[x])
ans+=dfs(x);
return ans ;// return the size
}
void solve(){
cin >> n >> m >> k ;// input stuff
For(i,m){
cin >>a >> b ;
friendship[a].em(b);
friendship[b].em(a) ;
}
For(i,k){
cin >>a>> b ;
blockship[a].em(b);
blockship[b].em(a) ;
}
mems(visited,0) ; // initialise all visited nodes as non visited
//Now traverse all nodes and check if it is visited or not if it is then you can be sure that it is part of some component
//that has already be processed else compute tha ans for all nodes of that particular component
for(int i =1;i<=n;i++){
if(visited[i])
continue ;
component.clear() ;// make sure to empty the set before moving ahead
int comp_size=dfs(i) ;// find size of the component which contains node i
for(int x :component){
ans[x]=comp_size-1 ;// first condition says that a!=b
for(int c:blockship[x])
if(component.count(c))ans[x]-- ;// second says that no blockship between a and b
ans[x]-=sz(friendship[x]) ;// lastly no friendship too
}
}
Rep(i,n)pff(ans[i]);// print the ans array
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
solve() ;
//ll t ; cin >> t ; while(t--)solve();
return 0;
}
Ping me if anything is not clear
I was solving the question since afternoon (with your help Ofcourse 
) and I can’t thank you enough. From example I got it fully understood. I was hoping someone would answer my question. Thank you for the detailed explanation. I really appreciate it.
Just a small help i further need, I wrote the code but I’m getting WA in 5 out of 30 test cases. 25 are showing AC, Here’s my commented solution Can You tell what is the mistake. Thank you very much once again 
Sure, just allow me some time
I was not able to find any flaw in the implementation of logic in first look but you may check these test cases where your solution is failing
12 7 52
8 11
11 3
9 6
7 6
6 4
11 4
11 12
12 10
1 7
8 2
3 1
8 1
8 9
8 3
1 2
12 5
8 5
10 4
10 7
8 4
7 11
5 6
12 9
12 7
7 9
5 10
6 3
12 3
5 7
11 5
9 11
2 3
12 6
3 5
10 6
8 12
2 10
2 12
11 6
8 6
3 9
3 4
5 1
3 7
12 4
10 11
9 5
11 1
7 8
7 4
2 7
9 4
10 9
1 9
10 8
9 2
6 1
4 1
2 4
18 41 71
14 9
13 1
1 18
6 5
9 1
2 17
12 18
3 13
10 11
6 4
14 7
11 7
4 1
5 18
4 8
6 2
6 14
4 13
9 11
8 3
17 14
1 14
13 17
11 3
16 1
15 2
13 5
9 10
7 18
5 17
4 14
17 4
1 11
2 18
13 16
2 11
15 7
5 2
12 2
15 9
2 3
14 13
6 3
18 14
1 17
5 14
11 16
18 8
12 8
12 11
2 10
4 18
5 10
12 13
5 11
8 10
10 4
6 18
1 2
11 18
6 1
7 12
10 12
16 5
3 18
15 3
5 3
15 11
14 15
15 5
11 14
15 18
11 13
14 8
6 7
12 6
5 7
1 5
7 2
12 15
10 15
12 17
8 15
16 12
8 7
2 9
11 6
17 16
4 2
3 9
18 10
9 5
6 10
12 14
14 3
10 13
9 6
11 4
11 8
4 3
1 3
17 8
18 9
9 13
3 7
17 6
17 7
4 12
15 17
8 2
8 6
16 3
17 46 55
11 7
11 9
17 15
14 8
15 7
7 9
12 5
16 3
3 10
5 15
2 16
3 4
10 12
10 4
8 17
5 1
13 6
15 12
1 2
8 7
1 8
2 10
14 11
15 8
8 3
17 5
3 2
2 11
9 8
5 16
10 7
11 3
13 1
7 12
14 4
4 17
4 13
12 11
11 4
6 11
1 7
2 6
14 10
12 8
14 6
12 6
7 13
11 1
13 11
5 10
6 5
1 4
17 9
14 1
16 15
2 14
1 6
5 3
13 5
5 8
15 11
17 3
10 8
6 4
3 9
11 8
13 2
13 9
4 16
9 14
15 10
1 12
5 14
4 2
8 6
3 7
3 6
9 2
7 4
8 4
6 15
13 16
3 15
16 9
14 3
15 4
16 6
6 10
9 4
10 11
1 16
12 2
17 6
5 2
16 10
7 2
8 13
10 9
9 5
17 2
1 10