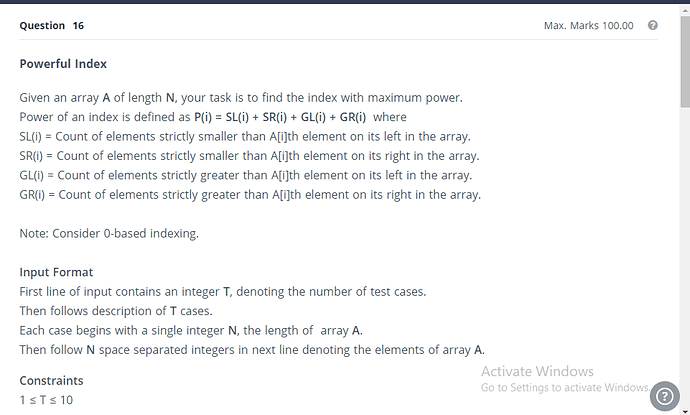
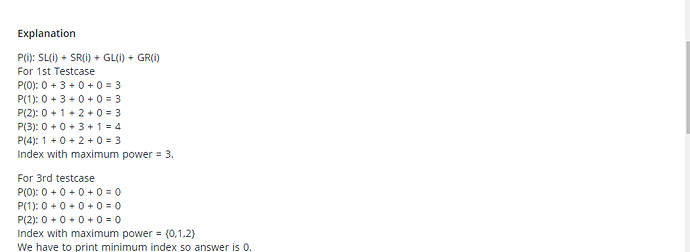Hiii everyone,
This was a problem from a completed Hackerearth hiring challenge.Link
Can anyone help in this problem. I have tried an O(n^2) method of writing 4 functions Sl,SR,Gl,GR and finding minimum of their sums. But my solution gave TLE. I thought of using Binary indexed tree which reduces complexity but could not implement it. Can anyone help in this problem @ssjgz @l_returns @aryanc403
I can’t see question on given link.
How can I verify if its from the link given by you ?
notice that, for an index i:
SL(i) + SR(i) = total number of elements in array less than A[i]
GL(i) + GR(i) = total number of elemets in array greater than A[i]
since in the end you have to anyways add sl, sr, gl and gr no need to calc each of them seperately, instead for each element of array find number of elements less than it and number of elements greater than it.
To do that also since in the end you only need maximum power, you can sort and find out for element. (by finding total occurance of the element. Power would be length of array - total occurances of element)
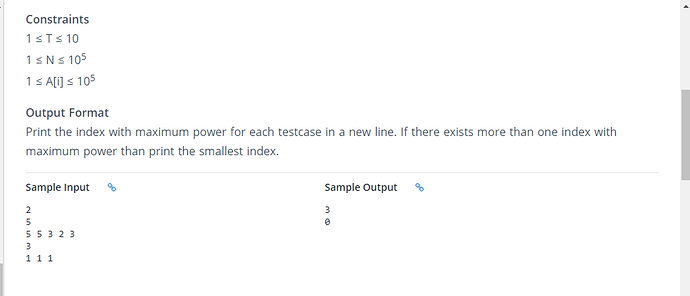
in the given test case
for element 2 - count = 1 => power = 5 - 1 = 4
for element 3 : count = 2 => powet = 5 - 2 = 3
you can see anywhere 3 is there in array, its power will be coming 3 only.
So in the end just find element having maximum occurances and then return length - count(maximum occuring element)
(Dont know if this is correct tho, please check)
You reached halfway to actual logic 
Correct
P(i) = strictly smaller + strictly greater
= N - freq of this element
Now for P(i) to be maximum.
Freq of element should be minimum.
Hence we need the element having minimum frequency.
In case freq of two element is same, the one with smallest index.
Let me if you can solve this in O(n) on your own. Or you need help. @rocky_1234
find frequency of each element using array F of 10^5+1 size ( F[a[i]]++ ).
Also store minimum index of each element.
Then just output answer in O(10^5)
