Help Needed to solve a Problem

[suman_18733097]

Here’s the Problem Statement.
Consider a M x N, two dimensional Grid. Two types of cells are defined - Blocked Cell and Free Cell, i.e., any cell is either blocked or free. Consider all Possible paths from top left cell (1,1) to bottom right cell (M,N) such that, at any cell, you can move either to the cell on its right, or to the cell below it. Now we define a special cell. A Special cell is a free cell such that, if it is blocked, then no path exists from (1,1) to (M,N). You are given the representation of grid in the form of a matrix where 1 represents a free cell and 0 represents a blocked cell. Find the probability that, if you pick a free cell, it is also a special cell.
Output Format: Say you can represent the Probability in the form of P/Q. Print P x Q^{-1} Modulo 10^9+7
Constraints: 1 \le M,N \le 10^3

Example input:
10 10
1110011001
1011100100
1101100010
0110100000
0011111000
0100010101
1000011011
0000001111
0000101011
0000101111
Example Output:
956521746

Explanation:

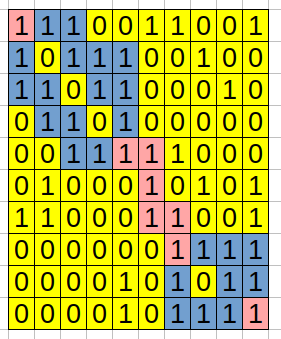
Non-Yellow cells constitute all possible paths from (1,1) to (10,10).
Cells in Pink represent Special Cells.
There are 46 Free Cells in total and 8 Special Cells in total. So, Probability is 8/46, viz., 4/23.
Now, The answer is (4 \times inverse(23)) \% (10^9+7)., viz., 956521746.

Any approach to solve this?

[cubefreak777]

Can you share the link?

[suman_18733097]

I don’t have the link. It was asked in SheCodes Technical round yesterday. My cousin attended the round and shared the questions after the round finished. Feel free to ask if anything is not clear.

[cubefreak777]

Why not just find the count of all articulation points in the graph?

[suman_18733097]

Thank you so much.

[suman_18733097]

The concept you shared is interesting. Indeed, I actually learnt two new Concepts. One being the Articulation Point, whose time complexity is O(M*N) (I mean, in this problem). The other was some new algorithm to me. I would like to talk about it later, after anyone shares their approach to solve this problem in O(M+N) time.

Anyone can share their approach along with some pseudo code to solve this problem in O(M+N) time.

[cubefreak777]

First of all, I need to apologize, Actually, I didn’t read the problem seriously back then and just suggested the first approach that came to my mind. Now if I think seriously then it’s clearly evident that this solution is totally incorrect and will fail most of the test-cases.
Now coming to the correct solution, here is the code of solution which I came up with and (I have proof that this one is correct ) it’s clean enough for you to read. Just ping me once if you don’t get the idea I’ll be happy to explain. Again sorry for wasting your time yesterday.

CORRECT_CODE

#include "bits/stdc++.h"
#define int long long 
using namespace std ;
const int M =1e9+7 ;
int pM(int b,int p){
  int r=1 ;
  for(;p;b=(b*b)%M,p/=2)
    if(p&1)
      r=(r*b)%M ;
  return r ;
}
signed main(){  
  int n,m,c=0,ans=0;
  cin>>n>>m ;
  vector<string>a(n) ;
  vector<vector<int>>dp(n+2,vector<int>(m+2)),dp1(n+2,vector<int>(m+2)) ;
  for(string &x:a)
    cin>>x ;

  dp[0][1]=1 ;
  for(int i=1;i<=n;i++)
    for(int j=1;j<=m;j++)
      if(a[i-1][j-1]=='1')
        dp[i][j]=(dp[i-1][j]+dp[i][j-1])%M,c++;

  dp1[n][m+1]=1 ;
  for(int i=n;i;--i)
    for(int j=m;j;--j)
      if(a[i-1][j-1]=='1')
        dp1[i][j]=(dp1[i+1][j]+dp1[i][j+1])%M ;

  for(int i=1;i<=n;i++)
    for(int j=1;j<=m;j++)
      ans+=((dp[i][j]*dp1[i][j])%M==dp1[1][1]) ;

  cout<<ans*pM(c,M-2)%M  ;

}

[suman_18733097]

Yeah, I get it. But what you shared recently is still an O(M*N) Solution. Can you come up with an O(M+N) Solution, with convincing approach?

[suman_18733097]

@cubefreak777

Now if I think seriously then it’s clearly evident that this solution is totally incorrect and will fail most of the test-cases.

Not exactly, I can indeed construct a graph having M * N vertices and can find the number of articulation points in O(M * N). But implementation becomes hectic.

@cubefreak777

Again sorry for wasting your time yesterday.

Not at all. I learnt new concept yesterday. I would like to thank you again.

[cubefreak777]

@suman_18733097

Not exactly, I can indeed construct a graph having M * N vertices and can find the number of articulation points in O(M * N).

Why go any far, so how many articulation points the sample test-case contains according to you ?

[suman_18733097]

Yeah, I know there are very few. It doesn’t matter to construct a graph or solve it using Dynamic Programming, when both of them are O(M*N). So, yeah, I wanted to know if you or anybody else can solve the same problem in O(M+N).

[cubefreak777]

No, I meant to say, is (1,1) an articulation point? No, it isn’t. All that we want is to have the cell (1,1) and (n,m) in different components after deleting a cell, but if we delete an articulation point then it’s nowhere ensured that [1,1] and [n,m] are in different components!!. For example consider this

1000
1111
0100
0111

here cell (2,3) (one-based indexing) is an articulation point because it disconnects the graph but if we after we delete it the disconnected graph would look like,

1000
1101
0100
0111

Now you see, we’ve removed an articulation point but [n,m] is still reachable from [1,1]

[suman_18733097]

Oh yeah. I didn’t consider that case. Interesting.
I asked one of my friends regarding the solution to this problem. He told one of the interesting solutions to this problem.

Before we go to the approach, we will define two algorithms.

1. RDFS: Stands for Rigth - Depth First Search. Unlike the naive DFS, this one prefers to go right always. If there is no way you can go right, then you’ll see if you can go down. If yes, proceed, else, the current cell is of no use (since you can’t go to the right and bottom), so, you’ll mark this cell 0 which was given as 1. Now, backtrack to the previous visited cell and continue exploring, until you visit (M,N) or you mark all visited cells 0.
   This tour gives us a path from (0, 0) to (M, N), say r_path.

2. DDFS: Stands for Down - Depth first search. Similar to RDFS, but this one prefers to go down always. If there is no way you can go down, you’ll see if you can go right. If yes, proceed. Otherwise, the current cell is of no use, you’ll mark it 0. Backtrack to the previous visited cell and continue exploring. Stop the tour after you visit (M,N) or you mark all visited cells as 0.
   This tour gives us another path, say d_path.

The Approach is as follows:
1, Find r_path and d_path. I was convinced with the following statement of my friend.
“These two paths will always try to be as far as possible. If they are still intersecting, then the points of intersection are indeed special”
2. Find the number of points where these two paths intersect. This gives us the number of special cells. The rest is trivial though.

We thought this algorithm would run in O(M+N) time. But for special cases of grid like the below one, the time complexity becomes O(M*N). But this approach is kinda interesting.

Example input for worst case of above algorithm.

M = N = 10

1111111111
1111111110
1111111100
1111111000
1111110000
1111100000
1111000000
1110000000
1100000001
1000000011

Both try to reach (10, 10) but can’t.

If you spot any error in the approach, please let me know.

[cubefreak777]

Nice solution and I think we can prove that it’ll work for all cases. Now I’ll give my approach to this problem using some trivial dynamic programming:
So first let’s count the number of paths from the cell [1,1] to [n,m], which can be done with a very trivial dp like this:

// dp[i][j] is number of ways to reach cell [i][j] from cell [1,1] 
for(int i=1;i<=n;i++)
    for(int j=1;j<=m;j++)
         if(a[i][j]=='1')
              dp[i][j]=dp[i-1][j]+dp[i][j-1] ;

Now with this dp we will get the number of paths from [1,1] to [n,m], i.e. dp[n][m]
Now Here’s a very interesting observation:

So all special cells will be a part of all dp[n][m] paths. 

We can prove this fact by contradiction :
Suppose there is a special cell [x,y] which is not a part of all dp[n][m] paths(which means something less than dp[n][m] , say A),i.e, even if we delete this cell then we will still have (dp[n][m]-A) paths between cell [1,1] and [n,m] which means [1,1] and [n,m] are still connected and [x,y] is not a special cell.
So now the only task at hand is to calculate the number of paths a cell is a part of out of the dp[n][m] paths. And it’s quite easy to compute.
Run a second dp1 from the cell [n,m] where

dp1[i][j] is  number of ways to reach cell [n,m] from cell [i,j]
for(int i=n;i;--i)
    for(int j=m;j;--j)
      if(a[i][j]=='1')
        dp1[i][j]=(dp1[i+1][j]+dp1[i][j+1]) ;

From basic combinatorics number of paths which a cell [i,j] is a part of will be ans[i][j] given by :

ans[i][j]=dp[i][i]*dp1[i][j]    (Number of ways to reach [i,j] * Number of ways to reach [n,m] from [i,j])

Now just count the number of cells which have their ans[i][j] value equal to dp[n][m] and you’ll be good to go.

CODE FOR REFERENCE

#include "bits/stdc++.h"
#define int long long 
using namespace std ;
const int M =1e9+7 ;
int pM(int b,int p){
  int r=1 ;
  for(;p;b=(b*b)%M,p/=2)
    if(p&1)
      r=(r*b)%M ;
  return r ;
}
signed main(){  
  int n,m,c=0,ans=0;
  cin>>n>>m ;
  vector<string>a(n) ;
  vector<vector<int>>dp(n+2,vector<int>(m+2)),dp1(n+2,vector<int>(m+2)) ;
  for(string &x:a)
    cin>>x ;

  dp[0][1]=1 ;
  for(int i=1;i<=n;i++)
    for(int j=1;j<=m;j++)
      if(a[i-1][j-1]=='1')
        dp[i][j]=(dp[i-1][j]+dp[i][j-1])%M,c++;

  dp1[n][m+1]=1 ;
  for(int i=n;i;--i)
    for(int j=m;j;--j)
      if(a[i-1][j-1]=='1')
        dp1[i][j]=(dp1[i+1][j]+dp1[i][j+1])%M ;

  for(int i=1;i<=n;i++)
    for(int j=1;j<=m;j++)
      ans+=((dp[i][j]*dp1[i][j])%M==dp1[1][1]) ;

  cout<<ans*pM(c,M-2)%M  ;