Question
- Given an N- ary tree with N nodes (N <= 500). Each nodes contains some value (val <= 100).
- We have to modify the tree such that for each node of the tree, all the subtree of that node should have the same sum.
- For modification, we can only reduce the values of the node.
- We have to achieve this with minimum number of reductions.
- We have to report the sum of the node values of the required tree.
My approach
- I created a directed graph to represent the tree
- I performed a dfs to calculate the sum of the initial tree given and stored it as maxSum.
- Next I created a 2D dp array with dimensions [N+1][maxSum+1]
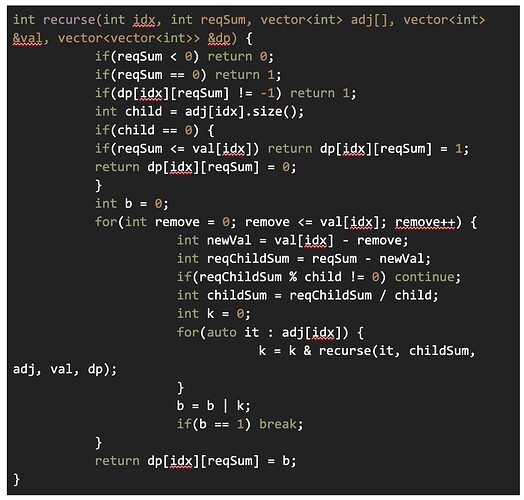
- Next I wrote a recursive a function that would take the node index and a sum and would return whether it is possible to achieve that particular sum in tree formed by that node and its subtree.
- Next I wrote a for loop that ran from maxSum to 0 and called the recursive function with parameters recurse(1->nodeIdx, requiredSum). If the recursive function returned true that that particular Sum would be my answer.
The boilerplate of my recursive function was like this:-
Verdict
This code was giving correct answer for the largest test case also, but on submitting overall it was giving TLE.
Can anyone tell a better approach to this problem that would pass within Time Limit ?