PROBLEM LINK:
Contest Division 1
Contest Division 2
Contest Division 3
Practice
Setter: Chaithanya Shyam
Tester: Utkarsh Gupta
Editorialist: Taranpreet Singh
DIFFICULTY
Medium
PREREQUISITES
Geometry, Divide and Conquer.
PROBLEM
There are N hidden points in a plane represented by array P, and you want to find the minimum squared distance between any pair of distinct points. In order to do that, you can ask at most 3*N-6 queries of the following form.
- ? i j: Returns the square of euclidian distance betwen points P_i and P_j.
QUICK EXPLANATION
- If we somehow figure out the coordinates of points, the problem reduces to finding the closest point pair which is a well-known problem.
- We can shift all the points in the plane without changing the relative distances between any pair of points. So we can assume the first point is at the origin.
- We can rotate all points in the plane without changing the relative distances between any pair of points, So we can assume the second point is (d_{12}, 0), where d_{12} is the distance between the first two points.
- Now, for each of the next points, we can compute its distance from the first and second points. Since the positions of the first and second points are fixed, the current point must be at the intersection of circles drawn from these two points. But there may be two points of intersection.
- We can choose any point when we get this situation the first time. Let’s say we get it when considering p-th point.
- Points 1, 2 and p can be used to uniquely determine the position of any other point in three queries.
EXPLANATION
This problem has two parts, identifying the points, and then computing minimum euclidian distance.
Finding All Points
Observation 1: We can shift all points in a plane without affecting the distance between any pair of points.
Let’s say x coordinates change by d_x and y coordinates change by d_y. Then the distance between points (x_1, y_1) and (x_2, y_2), which is \displaystyle \sqrt{(x_1-x_2)^2+(y_1-y_2)^2} must be same as distance between (x_1+d_x, y_1+d_y) and (x_2+d_x, y_2+d_y), which is true (can be verified easily).
Hence, we can assume that the first point is the origin.
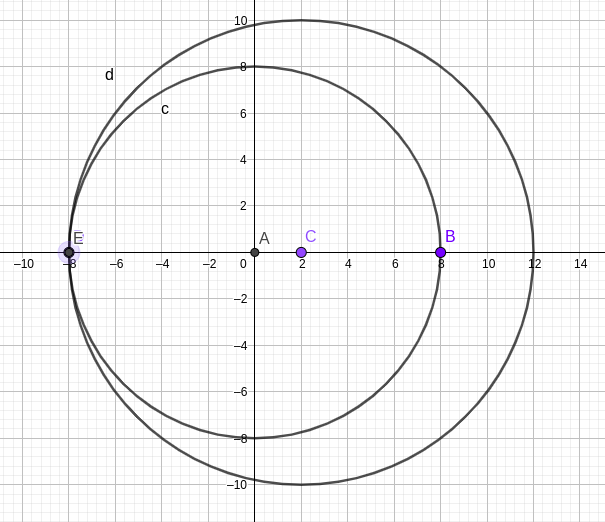
Now, let’s say we query the distance between the first and second points, say d_{12}. Where could the second point lie?
The set of points at distance d_{12} form a circle with center O and radius d_{12}.
Observation 2: We can rotate all the points by any angle centered at any point, without affecting the distance between any pair of points.
This way, we can choose any point on the circle as the second point, and the rest of the points would get rotated automatically.
Let’s say we know the first point is the origin and the second point is on X-axis. Considering the third point, let’s query its distance from the first two points, denoted by d_1 and d_2 respectively. We can see that the third point shall lie at the intersection of the circle with center at the first point with radius d_1 and circle with center at the second point with radius d_2.
One of the following cases arises
- If the point is on X-axis, we’d get a single point of intersection. That point of intersection is the coordinates of that point. A and C are first two points in this image, with d_1 = 8 and d_2 = 10
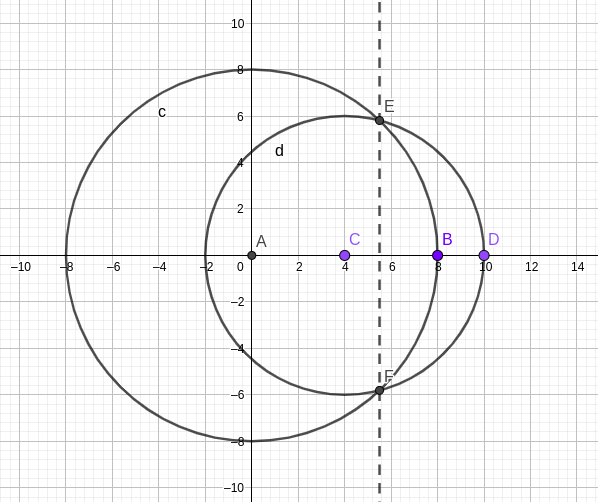
- If the point is not on X-axis, we’d get two points of intersection of these circles
Claim: When we second the situation for the first time, we can choose any of the two points as coordinates for the third point.
The effect of choosing E vs F is just reflecting all the points about X-axis.
Finding all points
Now that we have three Non-collinear points (Say A = (0, 0), B = (d_{12}, 0) and C not lying on X axis), we can uniquely recover all the remaining points.
Let’s say we query the distance of i-th point from A and B. Once again, we draw two circles, find two intersection points.
Claim: The two intersection points found shall be at an unequal distance from C.
Proof: The two intersection points would be of the form (x, y) and (x, -y). All points equidistant from these two points are on X-axis. but Point C is not on the X-axis.
Hence, if we query the distance of i-th point from C, we can uniquely identify which of the two coordinates are the valid choice for i-th point.
Number of queries taken
No queries asked for the first point (Since we assume it to be origin).
One query for the second point (distance to the first point).
Then two queries for each point until we find a point not collinear with the first two points.
Then three queries for each point.
In the worst case, we’d find a point not collinear with the first two points immediately. The number of queries taken would be 0+1+2+3*(N-3) = 3*N-6, which is the query limit.
Precision
Precision was a problem in this problem. Avoid the use of trigonometric operation, setter’s solution uses only Cosine rule and sqrt operation. Using long double is helpful.
Computing closest point pair
For the first subtask, we can use brute force to compute the distance between each pair of points and take minimum. But we can’t do that in the second subtask.
Given a set of N points in the cartesian plane, finding the smallest distance point pair is a well-known Divide and Conquer problem. One of the best resources to understand this would be here. This algorithm is also explained in the book CLRS Introduction to Algorithms.
Theoretical explanation here and implementation here
This step takes O(N*log(N)) time.
TIME COMPLEXITY
The overall time complexity is O(N*log(N)) per test case.
SOLUTIONS
Setter's Solution
#pragma GCC optimize("Ofast")
#pragma GCC target("avx,avx2,fma")
#include <bits/stdc++.h>
//#include <ext/pb_ds/assoc_container.hpp> //required
//#include <ext/pb_ds/tree_policy.hpp> //required
//using namespace __gnu_pbds; //required
using namespace std;
//template <typename T> using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
// ordered_set <int> s;
// s.find_by_order(k); returns the (k+1)th smallest element
// s.order_of_key(k); returns the number of elements in s strictly less than k
#define pb(x) push_back(x)
#define mp(x,y) make_pair(x,y)
#define all(x) x.begin(), x.end()
#define print(vec,l,r) for(int i = l; i <= r; i++) cout << vec[i] <<" "; cout << endl;
#define input(vec,N) for(int i = 0; i < (N); i++) cin >> vec[i];
#define leftmost_bit(x) (63-__builtin_clzll(x))
#define rightmost_bit(x) __builtin_ctzll(x) // count trailing zeros
#define set_bits(x) __builtin_popcountll(x)
#define pow2(i) (1LL << (i))
#define is_on(x, i) ((x) & pow2(i)) // state of the ith bit in x
#define set_on(x, i) ((x) | pow2(i)) // returns integer x with ith bit on
#define set_off(x, i) ((x) & ~pow2(i)) // returns integer x with ith bit off
#define fi first
#define se second
#ifdef LOCAL_DEBUG
#define debug(...) logger(#__VA_ARGS__, __VA_ARGS__)
#else
#define debug(...) ;
#endif
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
// auto dist = uniform_int_distribution<int>(l, r);
// use int a = dist(rng) to get a random number between [l,r] inclusive
template<typename ...Args>
void logger(string vars, Args&&... values) {
cerr << vars << " = ";
string delim = "";
(..., (cerr << delim << values, delim = ", "));
cerr << endl;
}
typedef long long int ll;
typedef long double ld;
const int MOD = 1e9+7; // 998244353;
const int MX = 2e5+5;
const ll INF = LLONG_MAX;
const ld PI = acos((ld)-1);
const ld EPS = 1e-6;
const int dx[4] = {1,0,-1,0}, dy[4] = {0,1,0,-1}; // for every grid problem!!
// highly risky #defines
#define int ll // disable when you want to make code a bit faster
#define double long double
// #define endl '\n' // disable when dealing with interactive problems
#define pdd pair<ld,ld>
#define pii pair<int,int>
typedef vector<int> vi;
inline ld getSqrt(ld d){
return sqrt(d);
// ld low = 0, high = 4e9;
// ld ans = -1, mid;
// for(int i = 0; i < 30; i++){
// mid = (low + high)/2.0;
// ld t = mid*mid;
// if(t > d) high = mid;
// else ans = low = mid;
// }
// assert(ans != -1);
// return ans;
}
class CPP{
vector<pdd> points;
public:
CPP(vector<pdd> points = {}){
this->points = points;
sort(all(this->points));// sorting by X
}
static bool cmpY(const pdd & a, const pdd & b) {
return a.second < b.second;
}
ld dist(int i, int j, vector<pdd> &v){
ld x = v[i].fi - v[j].fi;
ld y = v[i].se - v[j].se;
ld d = x*x + y*y;
return getSqrt(d);
}
void merge(vector<pdd> &v1, vector<pdd> &v2, ld &p){
vector<pdd> v;
ld mid = (v1.back().first + v2[0].first)/2.0;
for(pdd i: v1) if(abs(mid-i.first) <= p) v.pb(i);
for(pdd i: v2) if(abs(mid-i.first) <= p) v.pb(i);
int n = v.size();
sort(all(v), cmpY);
ld temp_p = p;
for(int i = 0; i < n; i++){
// below block is actually O(1)
// p x (p/2) block
for(int j = i+1; j <= i+8; j++){
if(j == n) break;
p = min(p, dist(i, j, v));
}
}
}
ld getCPPdist(vector<pdd> &pts){
int n = pts.size();
assert(n != 1);
if(n <= 3){
ld ans = INF;
for(int i = 0; i < n; i++){
for(int j = i+1; j < n; j++){
ans = min(ans, dist(i, j, pts));
}
}
return ans;
}
vector<pdd> v1, v2;
for(int i = 0; i < n/2; i++) v1.pb(pts[i]);
for(int i = n/2; i < n; i++) v2.pb(pts[i]);
ld p = min(getCPPdist(v1), getCPPdist(v2));
merge(v1, v2, p);
return p;
}
ld getCPPdist(){ return getCPPdist(points);}
};
//https://github.com/kth-competitive-programming/kactl/blob/main/content/geometry/Point.h
template <class T> int sgn(T x) { return (x > 0) - (x < 0); }
template<class T>
struct Point {
typedef Point P;
T x, y;
explicit Point(T x=0, T y=0) : x(x), y(y) {}
bool operator<(P p) const { return tie(x,y) < tie(p.x,p.y); }
bool operator==(P p) const { return tie(x,y)==tie(p.x,p.y); }
P operator+(P p) const { return P(x+p.x, y+p.y); }
P operator-(P p) const { return P(x-p.x, y-p.y); }
P operator*(T d) const { return P(x*d, y*d); }
P operator/(T d) const { return P(x/d, y/d); }
T dot(P p) const { return x*p.x + y*p.y; }
T cross(P p) const { return x*p.y - y*p.x; }
T cross(P a, P b) const { return (a-*this).cross(b-*this); }
T dist2() const { return x*x + y*y; }
double dist() const { return getSqrt((double)dist2()); }
// angle to x-axis in interval [-pi, pi]
double angle() const { return atan2(y, x); }
P unit() const { return *this/dist(); } // makes dist()=1
P perp() const { return P(-y, x); } // rotates +90 degrees
P normal() const { return perp().unit(); }
// returns point rotated 'a' radians ccw around the origin
P rotate(double a) const {
return P(x*cos(a)-y*sin(a),x*sin(a)+y*cos(a)); }
friend ostream& operator<<(ostream& os, P p) {
return os << "(" << p.x << "," << p.y << ")"; }
};
typedef Point<double> P;
bool circleInter(P a,P b,double r1,double r2,pair<P, P> &out) {
if (a == b) { assert(r1 != r2); return false; }
P vec = b - a;
double d2 = vec.dist2(),
sum = r1+r2,
dif = r1-r2,
p = (d2 + r1*r1 - r2*r2)/(d2*2),
h2 = r1*r1 - p*p*d2;
if (sum*sum < d2 || dif*dif > d2) return false;
P mid = a + vec*p, per = vec.perp() * getSqrt(fmax(0, h2) / d2);
out = {mid + per, mid - per};
return true;
}
ld dist(pdd p1, pdd p2){
ld x = p1.fi - p2.fi;
ld y = p1.se - p2.se;
return getSqrt(x*x + y*y);
}
int ask(int i, int j){
cout << "? " << i+1 << " " << j+1 << endl;
int t;
cin >> t;
assert(t > 0);
return t;
}
void answer(int ans){
cout << "! " << ans << endl;
}
pdd getCircleCircle(ld x1, ld r0, ld r1){
ld x = r0*r0 + x1*x1 - r1*r1;
x /= (2.0*x1);
ld y = max((ld)0, r0*r0 - x*x);
assert(y >= -(EPS*100));
y = max(y, (ld)0);
y = getSqrt(y);
return {x, y};
}
typedef Point<ld> P;
ld closest(vector<P> v) {
assert((int)v.size() > 1);
set<P> S;
sort(all(v), [](P a, P b) { return a.y < b.y; });
ld ret = LLONG_MAX;
int j = 0;
for (P p : v) {
P d{getSqrt(ret), 0};
while (v[j].y <= p.y - d.x) S.erase(v[j++]);
auto lo = S.lower_bound(p - d), hi = S.upper_bound(p + d);
for (; lo != hi; ++lo)
ret = min(ret, (*lo - p).dist2());
S.insert(p);
}
return getSqrt(ret);
}
ld distsq(Point<ld> p1, Point<ld> p2){
ld x = p1.x - p2.x;
ld y = p1.y - p2.y;
return x*x + y*y;
}
ld distsq(pdd p1, pdd p2){
ld x = p1.fi - p2.fi;
ld y = p1.se - p2.se;
return x*x + y*y;
}
int distsq(pii p1, pii p2){
int x = p1.fi - p2.fi;
int y = p1.se - p2.se;
return x*x + y*y;
}
void solve(int tt){
int N;
cin >> N;
vector<pdd> vec(N);
vec[0] = {0, 0};
vec[1] = {getSqrt(ask(0, 1)), 0};
int start = N;
for(int i = 2; i < N; i++){
ld r0 = getSqrt(ask(0, i));
ld r1 = getSqrt(ask(1, i));
Point<ld> a(0, 0), b(vec[1].fi, 0);
pair<Point<ld>, Point<ld>> intersect;
vec[i] = getCircleCircle(vec[1].fi, r0, r1); // not a generic template
if(start == N && vec[i].se > EPS) start = i; // first point above x axis
}
for(int i = start+1; i < N; i++){
pdd opp = vec[i];
opp.se = -opp.se;
ld d1 = dist(vec[start], vec[i]);
ld d2 = dist(vec[start], opp);
ld t = getSqrt(ask(start, i));
ld diff1 = abs(d1-t);
ld diff2 = abs(d2-t);
if(abs(diff1-diff2) < EPS) vec[i].se = 0;
else if(diff2 < diff1) vec[i].se = -vec[i].se;
}
vector<Point<ld>> temp;
for(int i = 0; i < N; i++) temp.pb(Point<ld>(vec[i].fi, vec[i].se));
ld ans = closest(temp);
ans *= ans;
answer(round(ans));
}
clock_t startTime;
double getCurrentTime() {
return (double)(clock() - startTime) / CLOCKS_PER_SEC;
}
signed main(){
ios_base::sync_with_stdio(false);
cin.tie(NULL);
startTime = clock();
// mt19937_64 rnd(time(NULL));
int T = 1;
cin >> T;
for(int t = 0; t < T; t++){
solve(t+1);
}
// cerr << "Time taken = " << getCurrentTime() << endl;
return 0;
}
Tester's Solution
#pragma GCC optimize("Ofast")
#pragma GCC target("avx,avx2,fma")
#include <bits/stdc++.h>
//#include <ext/pb_ds/assoc_container.hpp> //required
//#include <ext/pb_ds/tree_policy.hpp> //required
//using namespace __gnu_pbds; //required
using namespace std;
//template <typename T> using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
// ordered_set <int> s;
// s.find_by_order(k); returns the (k+1)th smallest element
// s.order_of_key(k); returns the number of elements in s strictly less than k
#define pb(x) push_back(x)
#define mp(x,y) make_pair(x,y)
#define all(x) x.begin(), x.end()
#define print(vec,l,r) for(int i = l; i <= r; i++) cout << vec[i] <<" "; cout << endl;
#define input(vec,N) for(int i = 0; i < (N); i++) cin >> vec[i];
#define leftmost_bit(x) (63-__builtin_clzll(x))
#define rightmost_bit(x) __builtin_ctzll(x) // count trailing zeros
#define set_bits(x) __builtin_popcountll(x)
#define pow2(i) (1LL << (i))
#define is_on(x, i) ((x) & pow2(i)) // state of the ith bit in x
#define set_on(x, i) ((x) | pow2(i)) // returns integer x with ith bit on
#define set_off(x, i) ((x) & ~pow2(i)) // returns integer x with ith bit off
#define fi first
#define se second
#ifdef LOCAL_DEBUG
#define debug(...) logger(#__VA_ARGS__, __VA_ARGS__)
#else
#define debug(...) ;
#endif
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
// auto dist = uniform_int_distribution<int>(l, r);
// use int a = dist(rng) to get a random number between [l,r] inclusive
template<typename ...Args>
void logger(string vars, Args&&... values) {
cerr << vars << " = ";
string delim = "";
(..., (cerr << delim << values, delim = ", "));
cerr << endl;
}
typedef long long int ll;
typedef long double ld;
const int MOD = 1e9+7; // 998244353;
const int MX = 2e5+5;
const ll INF = LLONG_MAX;
const ld PI = acos((ld)-1);
const ld EPS = 1e-6;
const int dx[4] = {1,0,-1,0}, dy[4] = {0,1,0,-1}; // for every grid problem!!
// highly risky #defines
#define int ll // disable when you want to make code a bit faster
#define double long double
// #define endl '\n' // disable when dealing with interactive problems
#define pdd pair<ld,ld>
#define pii pair<int,int>
typedef vector<int> vi;
inline ld getSqrt(ld d){
return sqrt(d);
// ld low = 0, high = 4e9;
// ld ans = -1, mid;
// for(int i = 0; i < 30; i++){
// mid = (low + high)/2.0;
// ld t = mid*mid;
// if(t > d) high = mid;
// else ans = low = mid;
// }
// assert(ans != -1);
// return ans;
}
class CPP{
vector<pdd> points;
public:
CPP(vector<pdd> points = {}){
this->points = points;
sort(all(this->points));// sorting by X
}
static bool cmpY(const pdd & a, const pdd & b) {
return a.second < b.second;
}
ld dist(int i, int j, vector<pdd> &v){
ld x = v[i].fi - v[j].fi;
ld y = v[i].se - v[j].se;
ld d = x*x + y*y;
return getSqrt(d);
}
void merge(vector<pdd> &v1, vector<pdd> &v2, ld &p){
vector<pdd> v;
ld mid = (v1.back().first + v2[0].first)/2.0;
for(pdd i: v1) if(abs(mid-i.first) <= p) v.pb(i);
for(pdd i: v2) if(abs(mid-i.first) <= p) v.pb(i);
int n = v.size();
sort(all(v), cmpY);
ld temp_p = p;
for(int i = 0; i < n; i++){
// below block is actually O(1)
// p x (p/2) block
for(int j = i+1; j <= i+8; j++){
if(j == n) break;
p = min(p, dist(i, j, v));
}
}
}
ld getCPPdist(vector<pdd> &pts){
int n = pts.size();
assert(n != 1);
if(n <= 3){
ld ans = INF;
for(int i = 0; i < n; i++){
for(int j = i+1; j < n; j++){
ans = min(ans, dist(i, j, pts));
}
}
return ans;
}
vector<pdd> v1, v2;
for(int i = 0; i < n/2; i++) v1.pb(pts[i]);
for(int i = n/2; i < n; i++) v2.pb(pts[i]);
ld p = min(getCPPdist(v1), getCPPdist(v2));
merge(v1, v2, p);
return p;
}
ld getCPPdist(){ return getCPPdist(points);}
};
//https://github.com/kth-competitive-programming/kactl/blob/main/content/geometry/Point.h
template <class T> int sgn(T x) { return (x > 0) - (x < 0); }
template<class T>
struct Point {
typedef Point P;
T x, y;
explicit Point(T x=0, T y=0) : x(x), y(y) {}
bool operator<(P p) const { return tie(x,y) < tie(p.x,p.y); }
bool operator==(P p) const { return tie(x,y)==tie(p.x,p.y); }
P operator+(P p) const { return P(x+p.x, y+p.y); }
P operator-(P p) const { return P(x-p.x, y-p.y); }
P operator*(T d) const { return P(x*d, y*d); }
P operator/(T d) const { return P(x/d, y/d); }
T dot(P p) const { return x*p.x + y*p.y; }
T cross(P p) const { return x*p.y - y*p.x; }
T cross(P a, P b) const { return (a-*this).cross(b-*this); }
T dist2() const { return x*x + y*y; }
double dist() const { return getSqrt((double)dist2()); }
// angle to x-axis in interval [-pi, pi]
double angle() const { return atan2(y, x); }
P unit() const { return *this/dist(); } // makes dist()=1
P perp() const { return P(-y, x); } // rotates +90 degrees
P normal() const { return perp().unit(); }
// returns point rotated 'a' radians ccw around the origin
P rotate(double a) const {
return P(x*cos(a)-y*sin(a),x*sin(a)+y*cos(a)); }
friend ostream& operator<<(ostream& os, P p) {
return os << "(" << p.x << "," << p.y << ")"; }
};
typedef Point<double> P;
bool circleInter(P a,P b,double r1,double r2,pair<P, P> &out) {
if (a == b) { assert(r1 != r2); return false; }
P vec = b - a;
double d2 = vec.dist2(),
sum = r1+r2,
dif = r1-r2,
p = (d2 + r1*r1 - r2*r2)/(d2*2),
h2 = r1*r1 - p*p*d2;
if (sum*sum < d2 || dif*dif > d2) return false;
P mid = a + vec*p, per = vec.perp() * getSqrt(fmax(0, h2) / d2);
out = {mid + per, mid - per};
return true;
}
ld dist(pdd p1, pdd p2){
ld x = p1.fi - p2.fi;
ld y = p1.se - p2.se;
return getSqrt(x*x + y*y);
}
int ask(int i, int j){
if(i>j)
swap(i,j);
cout << '?'<<' ' << i+1 << " " << j+1 << endl;
int t;
cin >> t;
return t;
}
void answer(int ans){
cout << '!'<<' ' << ans << endl;
}
pdd getCircleCircle(ld x1, ld r0, ld r1){
ld x = r0*r0 + x1*x1 - r1*r1;
x /= (2.0*x1);
ld y = max((ld)0, r0*r0 - x*x);
assert(y >= -(EPS*100));
y = max(y, (ld)0);
y = getSqrt(y);
return {x, y};
}
typedef Point<ld> P;
ld closest(vector<P> v) {
assert((int)v.size() > 1);
set<P> S;
sort(all(v), [](P a, P b) { return a.y < b.y; });
ld ret = LLONG_MAX;
int j = 0;
for (P p : v) {
P d{getSqrt(ret), 0};
while (v[j].y <= p.y - d.x) S.erase(v[j++]);
auto lo = S.lower_bound(p - d), hi = S.upper_bound(p + d);
for (; lo != hi; ++lo)
ret = min(ret, (*lo - p).dist2());
S.insert(p);
}
return getSqrt(ret);
}
ld distsq(Point<ld> p1, Point<ld> p2){
ld x = p1.x - p2.x;
ld y = p1.y - p2.y;
return x*x + y*y;
}
ld distsq(pdd p1, pdd p2){
ld x = p1.fi - p2.fi;
ld y = p1.se - p2.se;
return x*x + y*y;
}
int distsq(pii p1, pii p2){
int x = p1.fi - p2.fi;
int y = p1.se - p2.se;
return x*x + y*y;
}
void solve(int tt){
int N;
cin >> N;
vector<pdd> vec(N);
vec[0] = {0, 0};
vec[1] = {getSqrt(ask(0, 1)), 0};
int start = N;
for(int i = 2; i < N; i++){
ld r0 = getSqrt(ask(0, i));
ld r1 = getSqrt(ask(1, i));
Point<ld> a(0, 0), b(vec[1].fi, 0);
pair<Point<ld>, Point<ld>> intersect;
vec[i] = getCircleCircle(vec[1].fi, r0, r1); // not a generic template
if(start == N && vec[i].se > EPS) start = i; // first point above x axis
}
for(int i = start+1; i < N; i++){
pdd opp = vec[i];
opp.se = -opp.se;
ld d1 = dist(vec[start], vec[i]);
ld d2 = dist(vec[start], opp);
ld t = getSqrt(ask(start, i));
ld diff1 = abs(d1-t);
ld diff2 = abs(d2-t);
if(abs(diff1-diff2) < EPS) vec[i].se = 0;
else if(diff2 < diff1) vec[i].se = -vec[i].se;
}
vector<Point<ld>> temp;
for(int i = 0; i < N; i++) temp.pb(Point<ld>(vec[i].fi, vec[i].se));
ld ans = closest(temp);
ans *= ans;
answer(round(ans));
}
clock_t startTime;
double getCurrentTime() {
return (double)(clock() - startTime) / CLOCKS_PER_SEC;
}
signed main(){
ios_base::sync_with_stdio(false);
cin.tie(NULL);
startTime = clock();
// mt19937_64 rnd(time(NULL));
int T = 1;
cin >> T;
for(int t = 0; t < T; t++){
solve(t+1);
}
// cerr << "Time taken = " << getCurrentTime() << endl;
return 0;
}
Feel free to share your approach. Suggestions are welcomed as always. ![]()