PROBLEM LINK:
Practice
Div-2 Contest
Div-1 Contest
Author: Jatin Yadav
Tester: Chaithanya Shyam
Editorialist: Jatin Yadav
DIFFICULTY:
MEDIUM
PREREQUISITES:
None
PROBLEM:
There is an N \times N matrix with a hidden cell (a, b) not lying on its boundary. You can ask queries, in which you give the judge a matrix M of size N \times N, consisting of zeroes and ones. Let’s call a cell (i, j) valid if (i, j) = (a, b) or M[i][j] = 1. The judge replies whether there exists a path from (0, 0) to (N - 1, N - 1) consisting of only valid cells, and going either down or right. You need to find the hidden cell.
EXPLANATION:
Let’s use white for cells with M[i][j] = 0 and blue for cells with M[i][j] = 1. Clearly, It is of no use to query a matrix that already has a path from (0, 0) to (N - 1, N - 1) consisting only of blue cells (let’s call such a path a valid path from now on). Otherwise, the judge returns 1 if and only if the hidden cell was initially colored white, but if its color is changed to blue, then there will be a valid path.
Q=2N
We can find whether the hidden cell belongs to row i by having row i white and all other rows blue. Initially, there is no valid path. If any white cell’s color is changed to blue, there will be a valid path. So, the judge returns 1 if and only if the hidden cell was in row i.
So, we can simply query for every row whether the hidden cell is in that row. So, we can find the row number of the hidden cell in \le N queries. Similarly, we can also find the column number in \le N queries.
Code
from sys import stdin, stdout
def doesPathExist(s):
stdout.write("\n".join(["?"]+s+[""]))
stdout.flush()
return int(stdin.readline())
def isRow(r, N):
s = ["1" * N for i in range(N)]
s[r] = "0" * N
return doesPathExist(s)
def isCol(c, N):
return doesPathExist(["1" * c + "0" + "1" * (N - 1 - c) for i in range(N)])
def getRow(N):
for i in range(1, N - 1):
if(isRow(i, N)):
return i
return -1
def getCol(N):
for i in range(1, N - 1):
if(isCol(i, N)):
return i
return -1
Q=N + \log(N)
First find the column number (b). Now, to find the row number, we can binary search on it. Suppose we need to know whether the row number is \le r.
We’ll color the last column blue and the column b white. For all other columns, let’s color the cells with rows \le r blue and all others white. Then, there will be a valid path if and only if the row number, a \le r.
For example, if N = 8, b = 3, we can find if a \le 3 by querying :
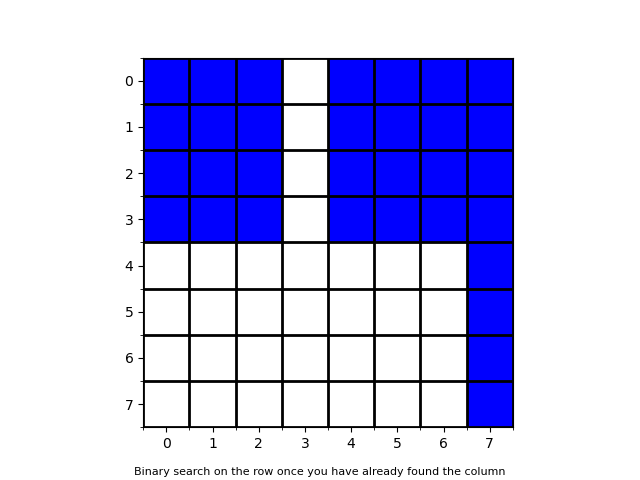
It takes \le N queries to find the column and then \le \log N queries to find the row. So, the total number of queries \le N + \log N
Code
def getRowBinarySearch(N, c):
lo, hi = 1, N - 2
while lo < hi:
r = (lo + hi) // 2
s = []
for i in range(N):
if i <= r:
s += ["1" * c + "0" + "1" * (N - 1 - c)]
else: s += ["0" * (N - 1) + "1"]
if doesPathExist(s): hi = r
else: lo = r + 1
return lo
Q=N
First, find if the cell lies on the main diagonal with one query. To do this, have all main diagonal entries and row 0 and N-1 white (except for (0,0) and (N-1, N-1).
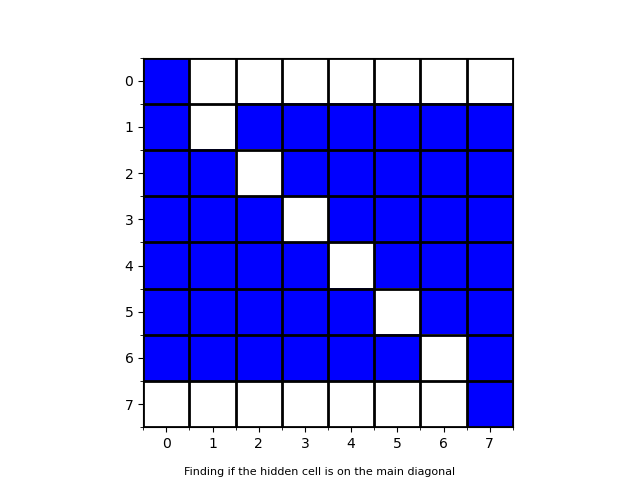
If the hidden cell is on the main diagonal, we can simply query its row number and total queries would be \le N.
Now, iterate over k from N - 2 down to 1 and have a cell (i, j) white if and only if \max(i, j) = k. The reply would tell us whether \max(a,b) = k.
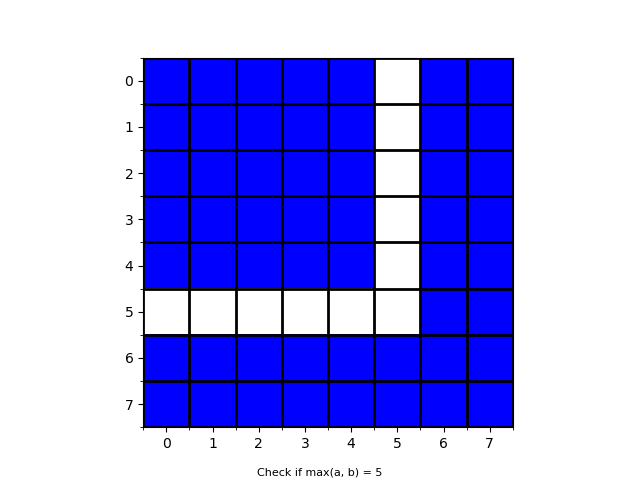
Now, once we get a positive result for some k, we can ask one query to find whether a = k or b = k. WLOG a = k. Then, we can make k - 1 more queries to find the column number. So, the total number of queries is \le 1(to find if main diagonal) + N - k - 1 (to find \max(a, b)) + 1 (to find whether a = k) + k-1 = N.
Code
# a = b?
def isMainDiagonal(N):
s = ["1" * i + "0" + "1" * (N - 1 - i) for i in range(N)]
s[0] = "1" + "0" * (N-1)
s[N - 1] = s[0][::-1]
return doesPathExist(s)
def findCell_N_Queries(N):
if isMainDiagonal(N):
for i in range(1, N - 1):
if isRow(i, N):
return (i, i)
for k in range(N - 2, 0, -1):
s = []
for i in range(N):
if i < k:
s += ["1" * k + "0" + "1" * (N - 1 - k)]
if i == k:
s += ["0" * (k+1) + "1" * (N - 1 - k)]
if i > k:
s += ["1" * N]
if doesPathExist(s):
# Check if the row number is k or the column number
if isRow(k, N):
for j in range(k - 1, 1, -1):
if isCol(j, N):
return (k, j)
return (k, 1)
else:
for i in range(k - 1, 1, -1):
if isRow(i, N):
return (i, k)
return (1, k)
return (-1, -1)
Q= 2\log(N)
In the solution with N + \log(N) queries, we first find the column in \le N queries and then the row in \le \log(N) queries. Ideally, we would want to also find the column in \le \log(N) + O(1) queries.
First, use 2 queries to find whether a \in \{1, N - 2\}. If so, find the column using binary search in that particular row (1 or N - 2). Otherwise, consider the problem:
You have a set S of columns, such that any two values in S differ by atleast 3. Find whether b \in S using a single query
To do this, have a cell (i, j) blue if and only if one of the following is true:
- i \in \{0, N - 1 \}
- j + 1 \in S and i \ne N-2
- j - 1 \in S and i \ne 1
For example, if N = 10, S = \{2, 6, 9\}, we have the following matrix:
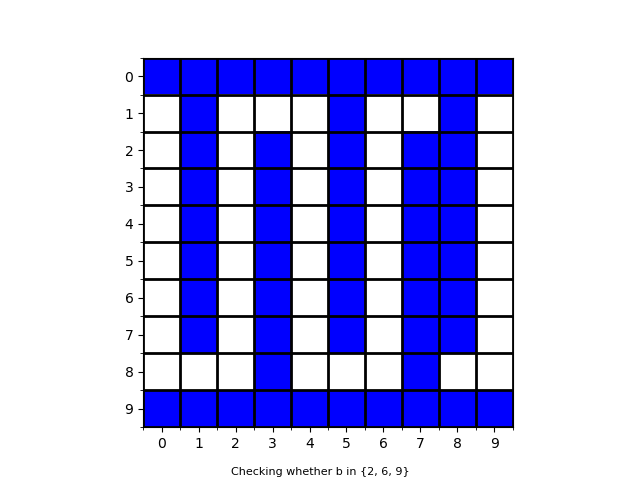
Then, b \in S if and only if the judge replies yes.
Let’s say that a cell (x_1, y_1) is reachable from (x_2, y_2) if there is a path of blue cells going right or down from (x_1, y_1) to (x_2, y_2) consisting of only blue cells. Let’s call a cell (i, j) interesting if i > 1 and i < N - 2. We have 4 types of columns j:
-
j \in S; all interesting cells in this column are white.
-
j + 1 \in S; All interesting cells in this column are reachable from (0, 0), but (N-1, N-1) is not reachable from these cells.
-
j - 1 \in S; (N-1, N-1) is reachable from all interesting cells of this column, but none of these cells is reachable from (0, 0).
-
All other remaining columns; All interesting cells in these are white. Even if an interesting cell in this column is changed to blue, it still won’t be reachable from (0, 0). This is because, if j's distance to largest column \le j in S was greater than 2, then the previous cell, (i, j-1) was also white. Else, the previous cell belonged to a column of type 3, and hence was not reachable from (0, 0).
Note that there is no valid path initially. Since we have already excluded the possibility of a \in \{1, N - 2\}, we know that our hidden cell is interesting.
If b \in S, clearly b - 1 is a column of type 2 and b + 1 is a column of type 3. So, we can go (0, 0) \rightsquigarrow (a, b - 1) \rightarrow (a, b) \rightarrow (a, b + 1) \rightsquigarrow (N-1, N-1). So, the judge replies with yes.
If b \notin S, if b had type 2 or 3, (a, b) was already colored blue and the judge replies no. Else, b is a type 4 column and (a, b) won’t be reachable from (0, 0) even after changing its to blue and the judge replies with no.
So, first let’s divide the initial potential set of columns \{1, 2, \ldots, N - 2\} into 3 sets according to j modulo 3. Then we can find which of the three sets b belongs to, in 2 queries. Then, binary search until we are left with only one potential column. Once we have found the column, we can binary search for the row. The total number of queries asked \approx 2 \log(N).
SOLUTIONS:
Setter's Solution
from sys import stdin, stdout
def doesPathExist(s):
stdout.write("?\n" + "\n".join(s)+"\n")
stdout.flush()
return int(stdin.readline())
def isRow(r, N):
s = ["1" * N for i in range(N)]
s[r] = "0" * N
return doesPathExist(s)
def getColBinarySearch(N, a):
lo, hi = 1, N - 2
while lo < hi:
c = (lo + hi) // 2
s = ["0" * N] * N
s[N - 1] = "1" * N
for i in range(0, N - 1):
if i != a:
s[i] = "1" * (c + 1) + "0" * (N - 1 - c)
if doesPathExist(s): hi = c
else: lo = c + 1
return lo
def getRowBinarySearch(N, c):
lo, hi = 1, N - 2
while lo < hi:
r = (lo + hi) // 2
s = []
for i in range(N):
if i <= r:
s += ["1" * c + "0" + "1" * (N - 1 - c)]
else: s += ["0" * (N - 1) + "1"]
if doesPathExist(s): hi = r
else: lo = r + 1
return lo
def isOneOfCols(N, S):
s = []
inS = [False] * N
for j in S: inS[j] = True
for i in range(N):
if i == 0 or i == N - 1: s += ["1" * N]
else:
temp = ""
for j in range(N):
if j != N - 1 and inS[j + 1] and i != N - 2:
temp += "1"
elif j != 0 and inS[j - 1] and i != 1:
temp += "1"
else: temp += "0"
s += [temp]
return doesPathExist(s)
def findHiddenCell(N):
if isRow(1, N):
return (1, getColBinarySearch(N, 1))
if isRow(N - 2, N):
return (N - 2, getColBinarySearch(N, N - 2))
cols = [[] for j in range(3)]
for j in range(1, N - 1): cols[j % 3].append(j)
id = 0
if isOneOfCols(N, cols[1]): id = 1
elif isOneOfCols(N, cols[2]): id = 2
S = list(cols[id])
while len(S) > 1:
L = len(S) // 2
A, B = S[:L], S[L:]
if isOneOfCols(N, A):
S = list(A)
else:
S = list(B)
return (getRowBinarySearch(N, S[0]), S[0])
for t in range(int(input())):
N = int(input())
r, c = findHiddenCell(N)
stdout.write("!\n")
stdout.write(str(r) + " " + str(c) + "\n")
stdout.flush()
res = stdin.readline()
assert(res != "-1")
Tester's Solution
#include <bits/stdc++.h>
using namespace std;
bool doesPathExist(const vector<string> & s){
cout << "?" << endl;
for(string ss : s) cout << ss << endl;
fflush(stdout);
int ret;
cin >> ret;
assert(ret != -1);
return ret;
}
#include <bits/stdc++.h>
using namespace std;
#define pb push_back
typedef vector<int> vi;
typedef vector<vi> vvi;
void print(vector<string> s){
for(int i = 0; i < (int)s.size(); i++){
if(i < 10) cerr << " ";
cerr << i << ") ";
cerr << s[i] << endl;
}
cerr << endl;
}
vector<string> getEmptyCol(int col, int N){
vector<string> ans(N, string(N, '1'));
for(int i = 0; i < N; i++) ans[i][col] = '0';
return ans;
}
vector<string> getEmptyRow(int row, int N){
vector<string> ans(N, string(N, '1'));
for(int i = 0; i < N; i++) ans[row][i] = '0';
return ans;
}
vector<string> getRowMatrix(int l, int r, int col, int N){
vector<string> ans(N, string(N, '0'));
for(int i = 0; i <= r; i++) ans[i][0] = '1';
for(int i = l; i < N; i++) ans[i][N-1] = '1';
for(int i = l; i <= r; i++){
for(int j = 0; j < N; j++){
if(j == col) ans[i][j] = '0';
else ans[i][j] = '1';
}
}
return ans;
}
int vertBS(int ans_y, int N){
int low = 0, high = N-1, mid;
while(low < high){
mid = (low+high)/2;
vector<string> temp = getRowMatrix(low, mid, ans_y, N);
if(doesPathExist(temp)){
high = mid;
}else{
low = mid+1;
}
}
return low;
}
vector<string> getColMatrix(int l, int r, int row, int N){
vector<string> ans(N, string(N, '0'));
for(int i = 0; i <= r; i++) ans[0][i] = '1';
for(int i = l; i < N; i++) ans[N-1][i] = '1';
for(int i = l; i <= r; i++){
for(int j = 0; j < N; j++){
if(j == row) ans[j][i] = '0';
else ans[j][i] = '1';
}
}
return ans;
}
int horiBS(int ans_x, int N){
int low = 0, high = N-1, mid;
while(low < high){
mid = (low+high)/2;
vector<string> temp = getColMatrix(low, mid, ans_x, N);
if(doesPathExist(temp)){
high = mid;
}else{
low = mid+1;
}
}
return low;
}
vector<string> getHorseMatrix(int col, int N, int spacing){
vector<string> ans(N, string(N, '1'));
for(int i = 1; i < N-1; i++){
for(int j = col; j < N-1; j += spacing){
ans[i][j] = '0';
}
} ans[N-1][col] = '0';
for(int i = col+2; i < N; i++){
ans[N-2][i] = '0';
}
// hook
for(int i = 1; i < N-1; i++){
for(int j = col; j < N-1; j += spacing){
ans[1][j+1] = '0'; ans[N-2][j+1] = '1';
}
}
return ans;
}
pair<int,int> rec(int index, int spacing, int N){
if(index + spacing >= N-1) return {vertBS(index, N), index};
if(doesPathExist(getHorseMatrix(index, N, 2*spacing))) return rec(index, 2*spacing, N);
else return rec(index + spacing, 2*spacing, N);
}
pair<int, int> findHiddenCell(int N){
if(doesPathExist(getEmptyRow(1, N))){
return {1, horiBS(1, N)};
}
if(doesPathExist(getEmptyRow(N-2, N))){
return {N-2, horiBS(N-2, N)};
}
int spacing = 3;
if(doesPathExist(getHorseMatrix(1, N, spacing))) return rec(1, spacing, N);
if(doesPathExist(getHorseMatrix(2, N, spacing))) return rec(2, spacing, N);
else return rec(3, spacing, N);
}
int main(){
int t; cin >> t;
while(t--){
int n;
cin >> n;
auto it = findHiddenCell(n);
cout << "!" << endl;
cout << it.first << " " << it.second << endl;
int res; cin >> res;
}
}