PROBLEM LINK:
Author: Sergey Kulik
Tester: Kevin Atienza
Editorialist: Kevin Atienza
PREREQUISITES:
Graphs, eccentricity, central nodes
PROBLEM:
Given a connected undirected graph of N nodes and M edges, add at most 2N nodes and N(N-1) edges such that:
- All previously existing N nodes (which we call the historical nodes) are central nodes (i.e. has minimal eccentricity among all nodes), while the new ones are not.
- No edges are added between any two of the previously existing N nodes.
Some of the terms I used in the previous sentence are standard and I’m sure you can search them online if you’re unfamiliar ![]()
QUICK EXPLANATION:
It’s always possible to do so within the given constraints. Here’s one way to do it:
- Create four nodes, A, B, C, D. Add the edges A-B and C-D, and connect all N historical nodes to A and C. Now all historical nodes have eccentricity of 2, while the new nodes have eccentricity 3 or 4. This requires 4 nodes and 2N+2 edges, so this is valid for N > 3.
- If N < 3, or if N = 3 and M = 3, the graph is complete (due to the connectivity constraint), so there is nothing needed to be done (the graph is totally symmetric and thus eccentricities are the same).
- The only remaining case is N = 3 and M = 2, which can only be a simple path graph of length 2 (again due to the connectivity constraint). If the historical nodes are R-S-T with S in the middle of the path, then we add two nodes A, B and add three edges B-S, A-R, A-T. Now R, S and T have an eccentricity of 2 while A and B have an eccentricity of 3.
EXPLANATION:
Here we first define some terms.
The eccentricity of a node v, denoted \epsilon(v), is the greatest shortest path from v to any other node. (Note: \epsilon(v) coincides with d(v) in the problem statement, but \epsilon(v) but seems to be a more standard notation after a bit of internet searching :D) The radius r of a graph is the minimum possible \epsilon(v) among all nodes v. A node v is called a central node if its eccentricity is the minimum possible, i.e. \epsilon(v) = r.
The eccentricity can be very large (even in connected graphs). In path graphs of N nodes for example, the eccentricities of the nodes at the ends of the path are N-1. However, we can introduce some nodes and edges to the graph to force the eccentricity to be at most 2.
Let A be a new node. If we connect A to all the N historical nodes, then it can be shown that the eccentricity of each node is at most 2, because we can always pass through A to reach any other node, for a total of two edges! This makes our task a bit easier, because our goal is to make the eccentricities of the N historical nodes equal. The following illustrates this:

The problem with this is that some historical nodes may still have eccentricities of 1. But we can fix this! We add another node, B, connected to A, so all historical nodes will have eccentricities of 2 (because they are 2 edges away from B). Here’s an illustration:

But there is still a problem. The eccentricity of A is 1 while the eccentricity of B is 2, but we want them to exceed 2. But we can still fix this! We add two nodes C and D, connect all N historical nodes to C, and connect C and D. The following illustrates this:
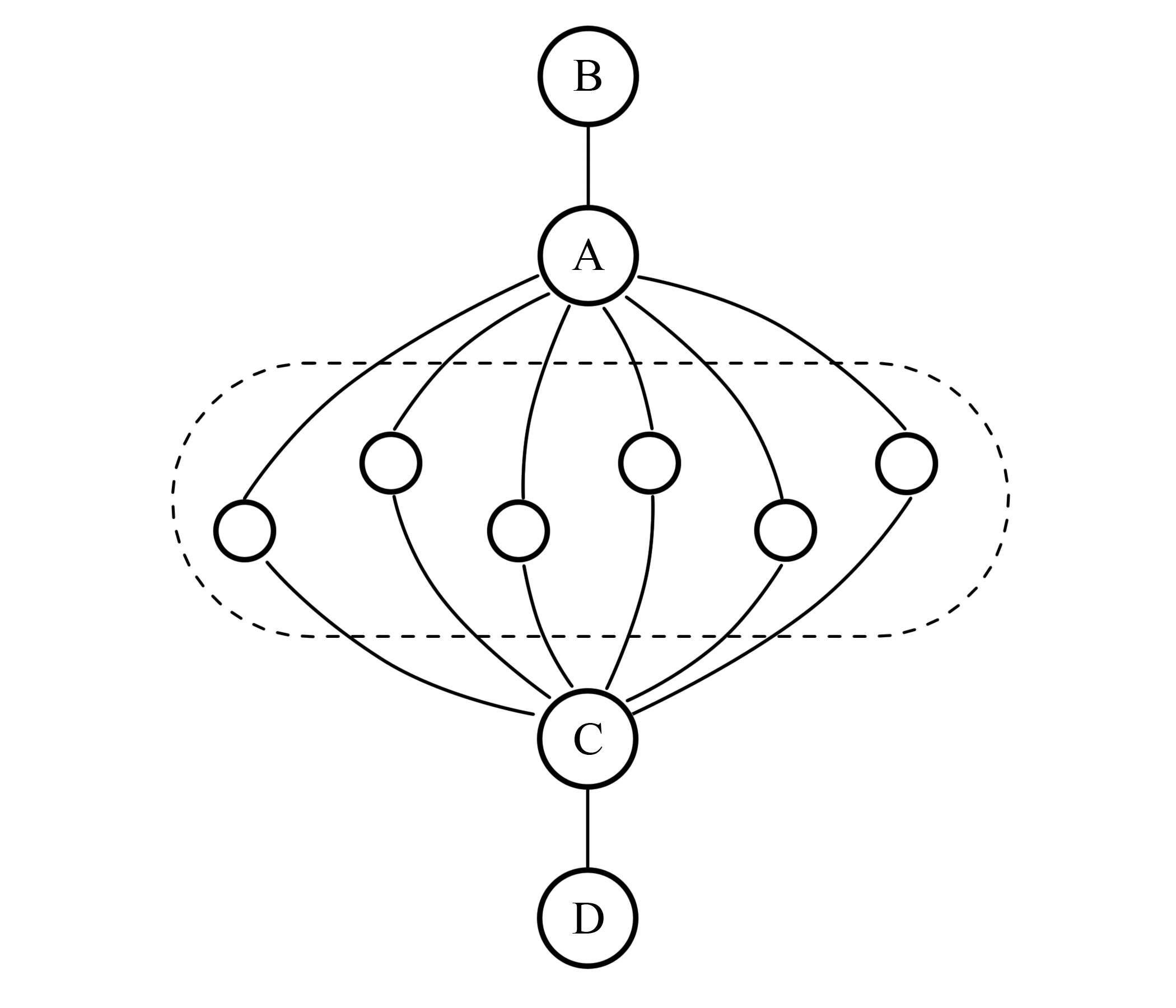
This will force A and B (as well as C and D) to have eccentricities at least 3, because there are nodes at the other side of the fence. Therefore, this construction is now valid! Also, note that we didn’t actually require the edge information, because they don’t really matter in this construction!
Now, let’s see how many nodes and edges we used. It’s easy to see that we have only added 4 nodes and 2N+2 edges. Now, we have a constraint to use at most 2N additional nodes and N(N-1) additional edges, but we have 4 \le 2N iff N \ge 2, and 2N+2 \le N(N-1) iff N \ge 4, so the construction above will work for all cases where N \ge 4 ![]()
We still have to consider the cases N \le 3 though. Thankfully, there are only four such cases, because the original graph is connected.
If N < 3, or if N = 3 and M = 3, it can be seen with some trial and error that the graph is complete, i.e. all pairs of nodes are connected by an edge (remember that the original graph is connected), so there is nothing needed to be done (the graph is totally symmetric and thus eccentricities are the same. In fact it is equal to 1 for N > 1 and 0 for N = 1 :D).
The only remaining case is N = 3 and M = 2, and there is only one such kind of graph: a simple path graph of length 2. Let’s call the three nodes in the path order as R, S and T (i.e. S is the middle). We cannot do the construction above because we are limited to 6 additional nodes and 6 additional edges. You can try to find a good construction in paper, but you can also do a brute-force search to find a valid construction. The first construction that came up in the editorialist’s brute-force search is what we will call the umbrella graph (![]() :D), i.e. the following
:D), i.e. the following
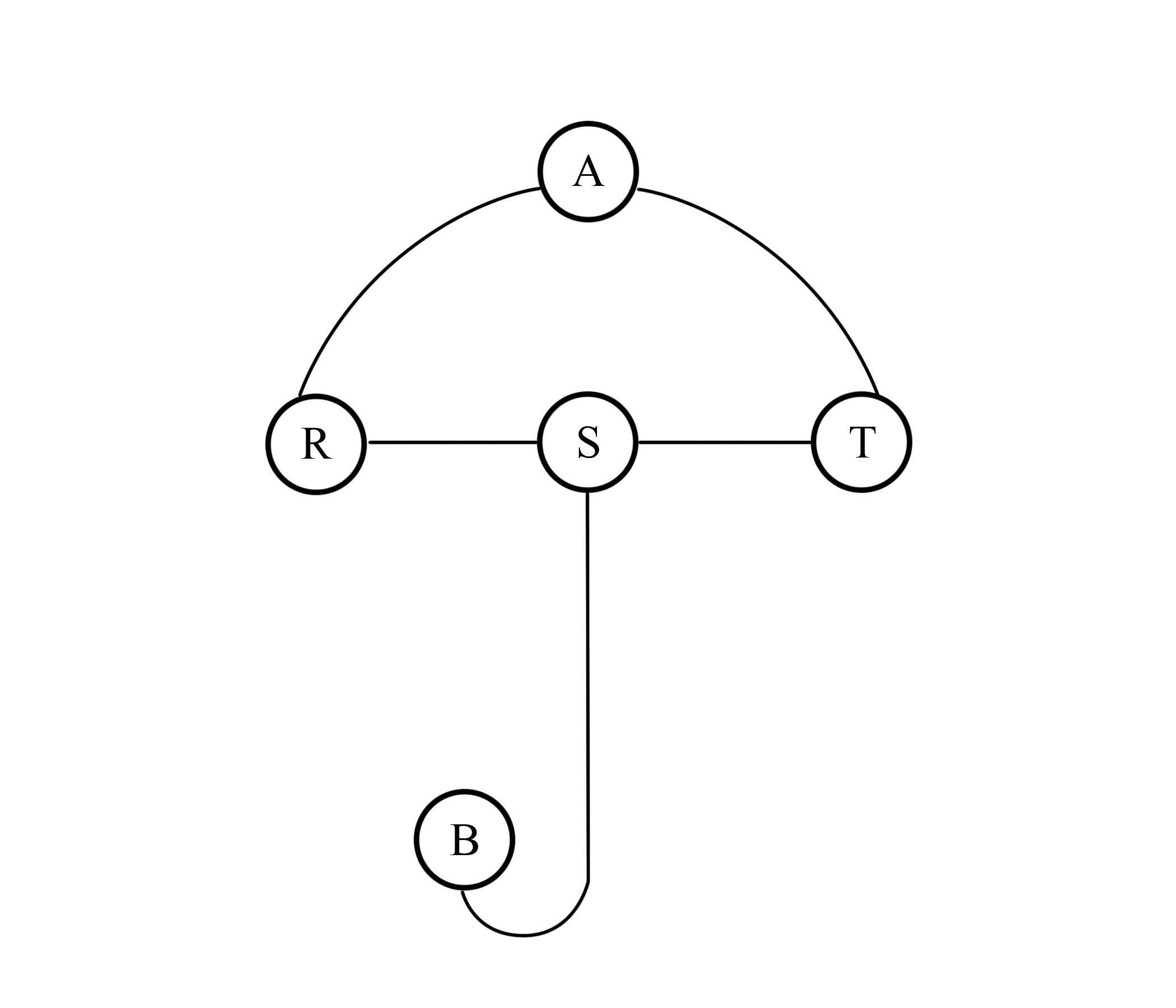
where the nodes A and B are new. It can be seen that the eccentricities of R, S and T are 2, while the eccentricities of A and B are 3. Moreover, there are only 2 additional nodes and 3 additional edges. Therefore, this is valid!
The time complexity of the whole algorithm is O(N+M), which is dominated by reading the input and writing the output. Also, since we didn’t miss any case, we have just shown that there always exists a solution.
Note: there are other constructions aside from what is described in this editorial. We have just shown you one possible way. We’d be happy to hear what you did ![]()
Time Complexity:
O(N+M)
