The Hare and the Tortoise race
We all have heard the story of the hare and the tortoise. Last time the hare lost the race to the tortoise because of his laziness. Since then the hare has been requesting the tortoise for a rematch numerous times and the tortoise has been always declining his request. Just a couple of days before the tortoise has agreed for a rematch on the condition that he will decide the route of the match.
A race between a hare and the tortoise has to happen on the hills of the Nilgiri forest. Nilgiri forest has N hills numbered from 1 to N. Some of these hills are connected by paths called forest paths. Since these paths can have sharp corners which can lead to two animals bumping into each other if they come from opposite directions, so the forest government have made them one-way.
You are given the time taken by the tortoise and the hare to move along a road for every forest road. Nilgiri has total M forest roads which are unidirectional.
The race can start from any hill but it should also end on the same hill. In other words, the path of the race should be cyclic.
The tortoise is now thinking of the route to take which involves the minimum number of roads and the tortoise is strictly faster than the hare on this route. If there are multiple such routes, the tortoise will choose the one which leads to the tortoise winning by the biggest margin (so that the hare doesn’t dare to challenge the tortoise again in future).
It is guaranteed that such a route always exists.
Input Format
The first line contains 2 space-separated integers N and M representing the number of hills and the number of forest roads.
Next follows M lines. The ith line contains 4 integers ui, vi, ti, hi - ui and vi represents the starting and ending hills of a forest road respectively, ti and hi represents the time taken to cross this road by the tortoise and the hare respectively.
Constraints
2 <= N <= 4
2 <= M <= N(N-1)
1 <= ui, vi <= N (ui != vi)
0 <= ti, hi <= 1000,000,000
Output Format
You have to print two space-separated integers - the first one is the minimum number of roads in the chosen path, and the second one is the biggest margin by which the tortoise can win the race on the chosen route.
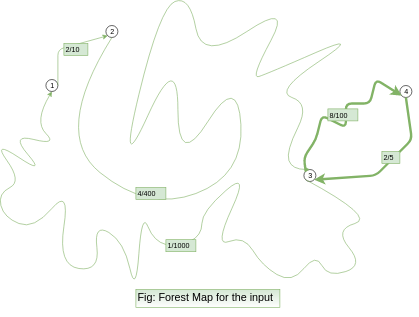
Sample TestCase 1
Input
4 5
1 2 2 10
2 3 4 400
3 4 8 100
4 3 2 5
3 1 1 1000
Output
2 95
You can see, the best route is 3 —> 4 ----> 3 which consists of 2 roads only. The margin by which the tortoise wins = (100 + 5) - (8 + 2) = 105 - 10 = 95.