Problem
I got the idea that we need to precalculate all the primes upto n, and for each prime p, we have to somehow find out the maximum power of p that occurs in our AF(n). Probably the concept of legendre’s formula can help. But I can’t really grasp the final equations.
Nice problem!
Here is what i did.
for a prime p where p \leq n
i can calculate how many times p^1 occurs, p^2 occurs and so on upto some p^k where p^k\leq n but p^{k+1} > n
it will only take log_p(n) time for a p.
you can visualize FA(4) as 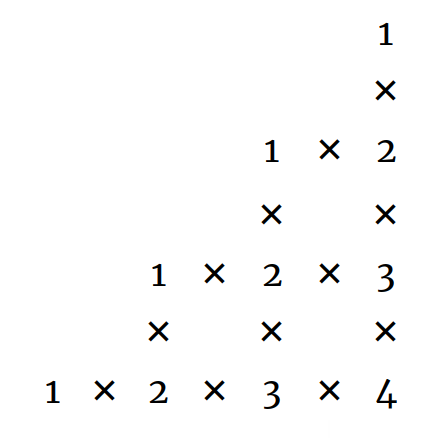
and you can generalise
\displaystyle \\
FA(n) = \prod_{i=1}^{n}i^{(n-i+1)}
hence if some prime factor p occurs as prime factor for some i then power of that p in FA(n) will be p^{n-i+1}
that is bit tricky. but all prime factors raised to some power e will occur \displaystyle\lfloor\frac{n}{p^e}\rfloor times in range [1,n].
you can make a relation for what should be power of the ith multiple of our p^e.
how i calculated
for simplification i assume it all as sum of integers upto \displaystyle\lfloor\frac{n}{p^e}\rfloor integers, and all the integers are multiplied with p^e.
\text{eggxample:}\\
n=4, \\
\text{in range [1,n] these elements occur}\\
1,2,3,4\\
\text{you can read sum of multiples of 2 as }(1+2) \times 2\text{ instead of (2 + 4)}
but by calculating in this manner i assumed every last occurance of p^e is at index n-p^e+1. (you can see 2 occurs at 2nd postions in above eggxample and should be (n - 1)th in range [1,n], which is not neccessary always correct. but the difference which it is going to add to answer is a constant. total difference in this manner as i calculated is abs(i - (n \>\bmod\> i) - 1) \times \lfloor\frac{n}{p^e}\rfloor.
and hence i can find power of each prime in FA(x).
total complexity O(n log(logn)) for Sieve buildup to calculate primes.
and O(p\times log_p(n)) to calculate powers of all primes in FA(n)
Code
#include <iostream>
#include <vector>
using namespace std;
const int mod=1e8+7;
const int N=5e6+2;
vector<bool> mark(N);
vector<int> prime;
long long n, ans, cur;
int main() {
for (int i=2; i<N; ++i) {
if (mark[i]) continue;
prime.push_back(i);
for (int j=i+i; j<N; j+=i)
mark[j]=1;
}
while(cin >> n, n) {
int ans=1;
for (int &p:prime) {
if (p > n) break;
cur=0;
for (long long i=p; i<=n; i*=p) {
long long k = n / i;
// sum of k integers * i ( current p^e ) * mod_inverse(2)
cur = (cur + (i * ((k * (k + 1)) % mod * 50000004 % mod)) % mod) % mod;
// subtracted k times abs(i - (n % i) - 1)
cur = (((cur - k * abs(i - (n % i) - 1)) % mod) + mod) % mod;
}
// prime p has power cur in FA(n)
ans = (cur+1) * ans % mod;
}
cout << ans << '\n';
};
return 0;
}