The AtCoder Beginner Contest 160 just ended and here I am with only two problems (the first two) solved. Though I think I figured out that problem E [Red and Green Apples] was a DP problem (a big thing for me to just figure this out as a beginner) I clearly messed it up with the implementation, I simply couldn’t convert the idea into code, and then I was also unable to use C++ as the array size was too large, so I decided to code in Python but nothing worked, I simply messed it up.
I think in problem E the DP only had one state, which I think was the total number of apples eaten so far where DP[i] is the deliciousness with i apples eaten so far, and the recurrence relation was DP[i] = DP[i-1] + max(p[last_index], q[last_index], r[last_index]). My idea was to take the max of the last element of each array, p, q and r after sorting them in ascending order. If max(p[last_index], q[last_index], r[last_index]) = p[last_index] then decrease X by one and delete the last element of p, if max(p[last_index], q[last_index], r[last_index]) = q[last_index] then decrease Y by one and delete the last element of q, if max(p[last_index], q[last_index], r[last_index]) = r[last_index] then decrease X by one if q[last_index] > p[last_index] else decrease Y by one. But then I ran into some out of bound type errors and so on.
Do you think my approach for problem E was correct? And how should I handle such large arrays in C++? Do you know some good forums where they publish editorials for these contests? And what your experiences in these contests, and how can I improve?
@everule1 What are your views?
I submitted D too gave TLE from test 12
It wasn’t a DP problem.
Simple AC array implementation of mine :
Sort all input arrays.
Now add all the last X elements from array p and last Y elements from array q.
This would be the solution if array C was empty.
So the smallest considered element from array p is p[A - X] and from q is q[B - Y]
Lets denote this indices as i and j.
Now start from the last element of array C and iterate backwards. For each element say curr,
IF curr < min(p[i], q[j])
BREAK
ELSE IF (p[i] < q[j])
Replace p[i] with curr
i++
ELSE i.e. q[j] < p[i]
Replace q[j] with curr
j++
You need to consider some cases when i reaches A and j reaches B but that will be doable I guess.
Cheers!
1 Like
A and B were very easy.
Question C
ans=k-max(max(a_{i+1} - a_i), k -a_n+a_1)
That’s because at most we can ignore at most one edge
Question D
You can literally create the graph, BFS every node and find the occurrence of every distance.
Time complexity is O(V(V+E)) which will pass, due to small constraints.
Question E
It is equivalent to At most x red apples, and at most Y apples, and greedily pick them.
Why?
If we pick k apples from red, Will it always be better to pick the k best ones.
Obviously yes.
Same can be said for colorless and green.
Either you’ll pick all the best ones, or if you’ve chosen all x from red or all y from green, you’ll still be picking the best possible, as the only ones that matter are the first x of red and first y of green, The rest are unchoosable.
Question F
is a bit difficult.
if dp[i] is the number of ways for i’s subtree with with respect to node 1 to have a value, Then
dp[i] = (size \ of\ subtree\ of\ i\ excluding\ i)! \times dp[j]/(size\ of\ subtree\ of\ j\ including\ j)! for all j as child of i.
We exclude i, as i will get 1 no matter what we do. Now to arrange them randomly, we get size(i)!. Now dp[j] are the number of orders that are allowed and size(j)! is the number of arrangements. And leaf nodes are set to 1.
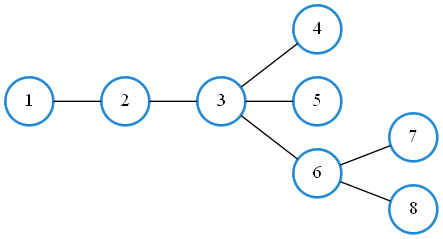
dp[6]=2! \times 1/1! \times 1/1!=2
that is because it’s either val[6]<val[7]<val[8] or val[6]<val[8]<val[7]. So 2 out of 6 sorts are possible.
dp[3]=5! \times 1/1! \times 1/1! \times 2/3! = 40
It’s 1/3 from dp[6] because 1 in 3 sorts violate the order and there are 5! random orders.
Now after we know it for 1, We can calculate it for some other node, connected to 1 with only 2 dp changes. If we want to go from i to j we only need to change dp[i] and dp[j], because if you look at it with the edge between them in the center of your graph, you’ll see that the rest of the dp relations will still be the same. You NEED to draw it to be able to see how that happens.
4 Likes
Nice ! The whole editorial in one post ! 
Can you please share your code for problem F?
The middle part is an absolute mess, and I don’t know how to make it better.
code
#include <iostream>
#include <bits/stdc++.h>
#include <cmath>
#include <vector>
#define ll long long int
#define mp make_pair
#define pb push_back
#define vi vector<int>
using namespace std;
vector<vector<int>> edge(200007);
vector<pair<ll,int>> dp(200007,mp(-1,0));
vector<ll> ans(200007);
vector<int> euler(400007);
vector<bool> vis(200007,0);
const ll p =1e9 + 7;
ll modpower(ll base, ll power, ll mod=p){
ll ans =1;
base%=p;
while(power){
if(power&1){
ans*=base;
ans%=p;
}
base*=base;
base%=p;
power>>=1;
}
return ans;
}
ll fact[200007];
ll invfact[200007];
void computefactorial(){
fact[0]=1;
for(int i=1;i<200007;i++){
fact[i]=i*fact[i-1];
fact[i]%=p;
}
invfact[200006]=modpower(fact[200006],p-2);
for(int i=200005;i>=0;i--){
invfact[i]=(i+1)*invfact[i+1];
invfact[i]%=p;
}
}
void eulerTree(int u, int &indx){ //Basic euler tree finder
vis[u] = 1;
euler[indx++] = u;
for (auto it : edge[u]) {
if (!vis[it]) {
eulerTree(it, indx);
euler[indx++] = u;
}
}
}
void solve(int u, int v){
if(dp[u].first!=-1){
return;//We've already calculated this
}
if(u!=v && edge[u].size()==1){
dp[u]=mp(1,1);//Leaf node, base state
return;
}
ll ans=1;
int size=0;
for(int i=0;i<edge[u].size();i++){
if(edge[u][i]==v){
continue;
}
//Go through all children and use the dp relations
solve(edge[u][i],u);
ans*=dp[edge[u][i]].first;
ans%=p;
ans*=invfact[dp[edge[u][i]].second];
ans%=p;
size+=dp[edge[u][i]].second;
}
ans*=fact[size];
ans%=p;
dp[u]=mp(ans,size+1);
return;
}
ll solve(){
int n;
cin>>n;
for(int i=0;i<n-1;i++){
int u,v;
cin>>u>>v;
edge[--u].pb(--v);
edge[v].pb(u);
}
solve(0,0);//Find dp[0] using the relations described above
ans[0]=dp[0].first;//ans is the final answer
int idx=0;
eulerTree(0,idx);
//make an euler tree to go to all the nodes in the tree
//So we find the answer for each node
for(int i=1;i<idx;i++){
//...
//First remove the last *fact[size] we did
/* ans*=fact[size];*/
dp[euler[i-1]].first*=invfact[dp[euler[i-1]].second - 1];
dp[euler[i-1]].first%=p;
//Since the new node and it's children are no longer part of the tree
//We remove them
dp[euler[i-1]].second-=dp[euler[i]].second;
//We multiply by fact[newsize]
dp[euler[i-1]].first*=fact[dp[euler[i-1]].second - 1];
dp[euler[i-1]].first%=p;
//Undo the multiplication with it's dp state
/*ans*=dp[edge[u][i]].first;*/
dp[euler[i-1]].first*=modpower(dp[euler[i]].first,p-2);
dp[euler[i-1]].first%=p;
//Undo /*invfact[dp[edge[u][i]].second];*/
dp[euler[i-1]].first*=fact[dp[euler[i]].second];
dp[euler[i-1]].first%=p;
//Now using the new value on the subtree we are rerooting to
//The size of this subtree increased so we have to undo
/*ans*fact[size]*/
dp[euler[i]].first*=invfact[dp[euler[i]].second - 1];
//add the NEW subtree of the previous one
dp[euler[i]].second+=dp[euler[i-1]].second;
dp[euler[i]].first%=p;
//Multiply by it's new size
dp[euler[i]].first*=fact[dp[euler[i]].second - 1];
dp[euler[i]].first%=p;
//use the normal dp relation
dp[euler[i]].first*=invfact[dp[euler[i-1]].second];
dp[euler[i]].first%=p;
dp[euler[i]].first*=dp[euler[i-1]].first;
dp[euler[i]].first%=p;
//We've found the answer for this node.
ans[euler[i]]=dp[euler[i]].first;
}
for(int i=0;i<n;i++){
cout<<ans[i]<<"\n";
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
computefactorial();//We'll need the factorial values.
solve();
}

