PROBLEM LINK:
DIFFICULTY:
EASY-MEDIUM
PREREQUISITES:
Number Theory
PROBLEM:
We have a laser placed at the top left corner of a rectangle with dimensions n*m. We need to find
how many boxes of unit area will be illuminated by the laser assuming that the rectangular edges are covered with mirrors.
EXPLANATION:
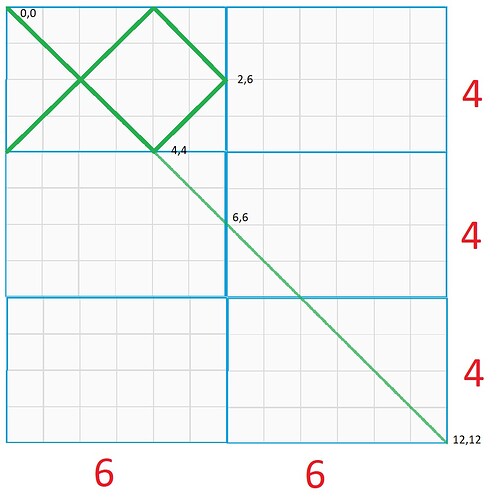
Consider the dimensions are n and m forming a quadrilateral ABCD (figure).
Consider n = 4 and m = 6
Following figure shows if we take a projection of a virtually forwarded ray, then it will strike a corner when the square is formed, so we want the length of the smallest square as answer.
This is the definition of the LCM in geometric form.
So the answer is LCM(n,m), and for this case its 12.
TIME COMPLEXITY :
The Time complexity is O(log(max(n,m)).
SOLUTION:
Solution
#include"bits/stdc++.h"
using namespace std;
#define int long long
void solve()
{
int n,m;
cin>>n>>m;
int g=__gcd(n,m);
cout<<(n*m)/g<<endl;
}
signed main()
{
ios_base::sync_with_stdio(0); cin.tie(0);
int tc=1;
cin>>tc;
for(int i=1;i<=tc;++i)
{
solve();
if(i<tc)
cout<<"\n";
}
return 0;
}