INOI 2020 question help

[sumit_king]

Hello community,
I need some help in this question : CodeChef: Practical coding for everyone
I am not able to solve this question for 100 pts. I need help for the third subtask.
It would be of great help if you could explain the idea behind the third subtask or give some hints.
Thank You

[aneee004]

Can you share your submission for the subtasks? Are you getting TLE or WA for larger constraints?

[sumit_king]

Hello @aneee004,
The constraints are not large. But, in the third subtask the value of k is different which leads to a different approach for that case. I am not able to think of that approach thats why it results in WA for that case.
My solution Link : CodeChef: Practical coding for everyone.
Thank You

[aneee004]

I think the transition is:
dp[i] = dp[i - 1] + dp[i - 3] + 2*dp[i - 6]
Looks like your adding dp[i - 6] only once. It is twice because you can either choose to fill the bottom row with two 1 X 3 tiles, or the top row with two 1 X 3 tiles.

Also, why are you calling tiles function in tiles1? Shouldn’t you be calling tiles1 again? (inside your if).

[sumit_king]

Thank You for your response,
That was a typo in which I was calling tiles in tiles1
My updated code : CodeChef: Practical coding for everyone
It still gives WA…
Can you tell why?

[therealnishuz]

Wrong approach.

[sumit_king]

Hey @therealnishuz,
Can you share your approach(If you know how to do this problem).

[therealnishuz]

My code:

#include <bits/stdc++.h>

using namespace std;

const int mod = 1e9+7, size = 1e6+1;

int main()
{
    ios_base::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    vector <long long> dp(size), f(size), g(size), h(size);
    dp[1] = 0;
    dp[2] = dp[3] = 1;
    f[1] = f[2] = 1;
    f[3] = 2;
    g[1] = 0;
    g[2] = g[3] = 1;
    h[1] = h[2] = 0;
    h[3] = 1;
    for (int i = 4; i < size; ++i) 
    {
        dp[i] = (dp[i-2] + dp[i-3]) % mod;
        f[i] = (f[i-1] + f[i-3] + 2*h[i-3]) % mod;
        g[i] = (f[i-2] + g[i-3]) % mod;
        h[i] = (g[i-1] + h[i-3]) % mod;
    }
    int t, k, n;
    cin >> t;
    while (t--)
    {
        cin >> k >> n;
        if (k == 1)
        {
            if (n % 3 == 0) cout << "1\n";
            else cout << "0\n";
        } else if (k == 2) cout << dp[n] << '\n'; 
        else cout << f[n] << '\n';
    }
}

If anything is not clear, ask me. Hopefully this will give you some hints.

[everule1]

The dp transitions are quite large but not difficult to figure out. Just remember you want to keep multiple dp states in each value.

Transitions

dp_{i,j} represents i columns filled with j tiles missing in the last column.

ans[i][2]+=ans[i-3][2];
ans[i][1]+=ans[i-1][2];
ans[i][0]+=ans[i-2][1];
ans[i][1]+=ans[i-3][1];
ans[i][2]+=ans[i-3][0]*2;
ans[i][0]+=ans[i-3][0];
ans[i][0]+=ans[i-1][0];

[aneee004]

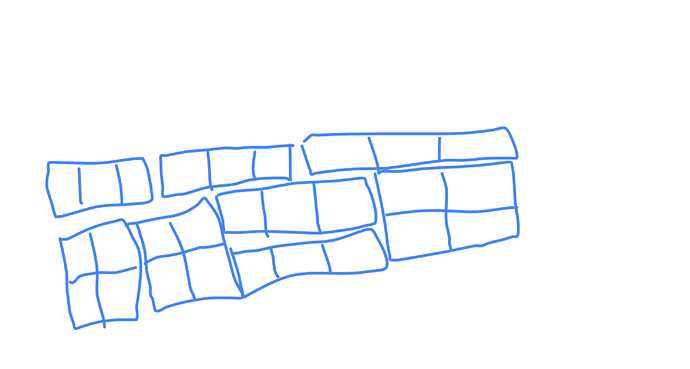
Yep. Just realized we can also fill it like this

Excuse the lousy drawing.
DAMN! That’s a lot of cases to deal with.

@everule1. Nice approach!

[sumit_king]

Thank You @everule1, @therealnishuz, and @aneee004 for helping

[therealnishuz]

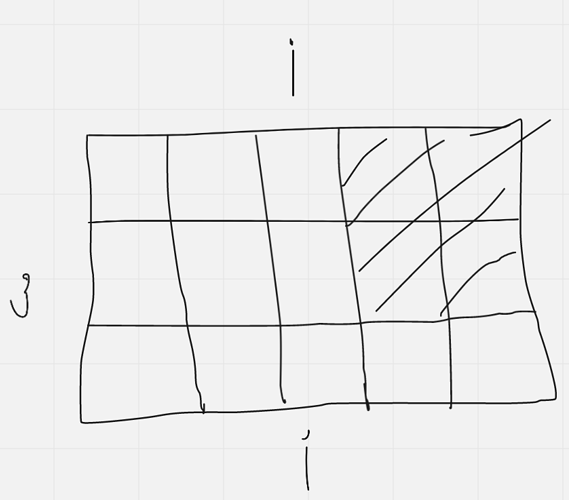
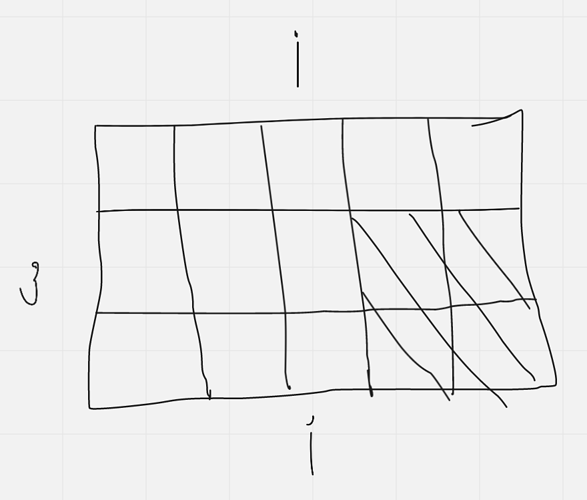
I’ll explain my solution.
Let’s say that f(i) is the number of ways that you can tile a 3 \times i block.
You can place a tile like this:

Or like this:

Or this:

Or this:

By symmetry, the last two are the same. If you tile it that way, you will be left with a 3 \times (i-3) block along with a 2 \times 1 block (because you’ll have to use a 1 \times 3 tile because you have to fill those gaps and you can’t do it with a 3 \times 1 tile and 2 \times 2 tile). Let’s say that the number of ways you can tile such a block is h(i-3).
Now f(i) = f(i-1) + f(i-3) + 2h(i-3)
I think that you can continue from here. Also, sorry for the terrible drawing.