Problem Link - Special Sums
Problem Statement
In this problem you are given two lists of N integers, a1, a2, ..., aN and b1, b2, ... bN. For any pair (i, j) with i, j ϵ {1, 2, ..., N} we define the segment from i to j, written as [i, j], to be i, i + 1, ..., j if i ≤ j and i, i + 1, ..., N, 1, 2, ...,j if i > j. Thus if N = 5 then the [2, 4] = {2, 3, 4} and [4, 2] = {4, 5, 1, 2}.
With each segment [i, j] we associate a special sum SSum[i, j] as follows:
- SSum[i, i] = ai.
- If i ≠ j then,
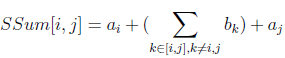
The positions i and j contribute ai and aj, respectively, to the sum while every other position k in [i, j] contributes bk.
Approach
To solve the problem, the logic involves handling the circular nature of the arrays. We first extend both a and b by appending their values to themselves, effectively doubling their length. This allows us to handle the wrap-around nature of segments [i,j] directly. We compute a prefix sum array for b to quickly calculate the sum of b- values in any segment. A deque is used as a sliding window to keep track of potential starting points i for the maximum SSum[i,j]. For each ending index j, we calculate the possible SSum[i,j] by considering the best starting index from the deque. The deque is maintained to ensure it always provides the maximum SSum for valid starting points within the range.
Time Complexity
The solution runs in O(N) due to the single traversal of the extended arrays and efficient deque operations.
Space Complexity
The space complexity is O(N), as we use arrays and a deque proportional to the input size.