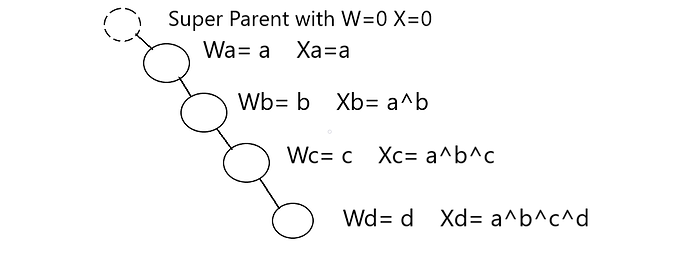Please read completely before having doubts.
First of all the condition 3&4 basically indicates that you can add a vertex with the parent as the closest vertex just above the this one which has Weight >= Weight of the newly added vertex. We can achieve this through the use of LCA.
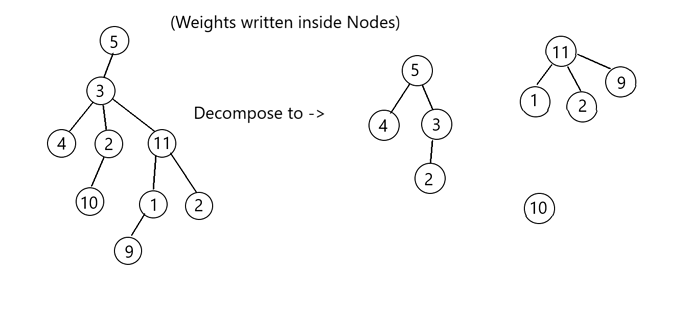
Lets see a sample graph… we can transform this into another graph (which can be disjoint)
From now on we will refer to this graph instead of original graph.
Now Before proceeding further please try to solve this question- Given N numbers and
Q queries, for each query output the maximum XOR achievable by XORing it with any of the N numbers. Its basically solvable by Trie. Here is another little harder version which I found SPOJ.com - Problem XORX . I cant seem to find the other question anywhere, If someone could find it the please paste it in comments.
Now lets change how we are processing query a little bit… Now lets Xi is the Xor of the ith Node from its parent till this point in our graph.Here a sample figure.
Now you see if we do the xor between two nodes it is equivalent to xor between their paths. For eg xor between B and D gives c^d. Similarly Xor between A and D gives b^c^d. Can we obtain somehow the value a^b^c^d? No, We need to add an imaginary node with value of 0 as kind of super parent. Now xor between D and super parent gives a^b^c^d.
Now on instead of actual Weight W we will take the Xor form the parent till this node X for every node.
Now query for a Node changes to- We have a node with Value Xi and we need to find the Node q with smallest depth such that it satisfy Xq^Xi <= Weight mentioned in query. Our answer will be = depth of current node - Smallest depth of node (which follows the above property).
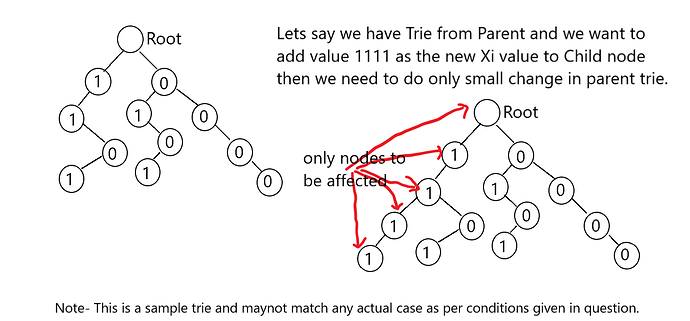
Lets have a idea on how to solve with a little optimization (although not whole idea). Now lets say If we have a sample tree then we for every Node will like to have a separate Trie which has all the the Xi values from parent till this node and leaves stores the depth of that node. If you have solve the above mentioned problem then u might have got the idea of how to solve this problem as well(or u can see the traverse function I have written in my code, also its better to think on how to solve this problem).
Now for complete Idea. Only thing missing was, we were making the trie for each node separately and that can cause memory overflow and time complexity issues. Lets say for any node which is not parent try to see changes in trie of this node and its parent… Assuming we are using 25 bits to represent each number( we can do it in 20 as well for given constraints). Then we can notice that the difference in DS of two nodes is of 25 nodes of Tries only (Nodes of Trie means the the Structure used in Trie). So if we have N nodes then actually we might only need around N*25 memory, this is the main idea and try thinking for yourself now for some moment. So what we will do is whenever we will add a Node with weight W and Xor Value from parent to Node X, we will have a pointer pointing to root of parent node and in current node we will Check if current bit in X is 1 or 0. If its 1 then the 0 part will stay same and we can simply point the 0th pointer of current Node to the 0th node pointed by parent and similarly, if current node has 0 then can do same for 1, i.e. point the 1th node of parent by the 1th pointer of current node, and now parent point should also move and point to next node (I.e. 0th or 1th depending on value of current bit of X to be 0 or 1 respectively).
For a new node not having a parent, remember adding value X as well as 0 (remeber our super parent). Super parent will be added only once for each seprate tree.
At last the inspiration for this question- Problem - D - Codeforces
Time Complexity: O(NlogN)
Memory Complexity: O(NlogW+NlogN)
My Soln
#include<bits/stdc++.h>
#include<math.h>
#define rep(i,k,n) for(int i=k;i<n;i++)
#define ll long long
#define MOD 1000000007ll
#define ROD 1000000007ll
#define INF 1e18
#define MIN(a,b) (a>b?b:a)
using namespace std;
#define mp make_pair
#define pb push_back
#define piii pair<pair<ll,ll>,ll>
#define pii pair<ll,ll>
#define fi first
#define se second
#define debug(…) fprintf(stderr, VA_ARGS), fflush(stderr)
#define time__(d)
for (
auto blockTime = make_pair(chrono::high_resolution_clock::now(), true);
blockTime.second;
debug(“%s: %lld ms\n”, d, chrono::duration_castchrono::milliseconds(chrono::high_resolution_clock::now() - blockTime.first).count()), blockTime.second = false
)
#define MAXN 200005
#define MAXV 1000001
typedef struct NODE
{
ll min_;
struct NODE zero,one;
NODE ()
{
zero=one=NULL;
min_=INF;
}
}NODE;
NODE nr[MAXN25], ptr[MAXN];
pii lr[MAXN][22],qr[MAXN][22];
ll q,wr[MAXN],pr[MAXN],depth[MAXN],xrwt[MAXN];
ll nw,ty,idx,wt,cur=1;
ll ww(NODE *,NODE *);
NODE *qq(NODE *);
NODE *add(NODE *,ll,ll,ll);
ll traverse(NODE *,ll,ll,ll,ll);
ll last=0;
int main()
{
cin>>q>>wr[1];
ptr[1]=add(ptr[1],0,19,0);
ptr[1]=add(ptr[1],wr[1],19,1);
depth[1]=1;
xrwt[1]=wr[1];
rep(i,0,q)
{
wt=0;
scanf("%lld %lld %lld",&ty,&idx,&wt);
if(ty==1)
{
cur++;
lr[cur][0].fi=idx;
lr[cur][0].se=wt;
wr[cur]=wt;
pr[cur]=idx;
xrwt[cur]=wt;
ll temp=idx,max_=wt;
// add for 1 as well
for(int i=1;i<20;i++)
{
lr[cur][i].fi=lr[temp][0].fi;
lr[cur][i].se=max(max_,lr[temp][0].se);
max_=max(max_,lr[temp][i].se);
temp=lr[temp][i].fi;
}
ll p=pr[cur];
for(int i=19;i>=0;i--)
{
if(lr[p][i].fi==0||lr[p][i].se>=wt)
continue;
p=lr[p][i].fi;
}
if(wr[p]<wt)
p=pr[p];
if(p==0)
{
// new tree being added
xrwt[cur]=wr[cur];
depth[cur]=1;
// super parent with value 0
ptr[cur]=add(ptr[cur],0,19,0);
// value for current Node
ptr[cur]=add(ptr[cur],xrwt[cur],19,1);
}
else
{
// add to old BIT tree
xrwt[cur]=(xrwt[p]^wr[cur]);
depth[cur]=depth[p]+1;
ptr[cur]=add(ptr[p],xrwt[cur],19,depth[cur]);
}
}
else
{
ll x=traverse(ptr[idx],19,1,wt,xrwt[idx]);
if(x>depth[idx])
x=depth[idx];
printf("%lld\n",depth[idx]-x);
last=depth[idx]-x;
}
}
}
NODE *add(NODE *ptr,ll val,ll idx,ll depth)
{
NODE *q=qq(ptr);
if(idx<0)
{
q->min_=min(q->min_,depth);
return q;
}
if(val&(1<<idx))
{
q->one=add(q->one,val,idx-1,depth);
}
else
{
q->zero=add(q->zero,val,idx-1,depth);
}
q->min_=ww(q->zero,q->one);
return q;
}
ll ww(NODE *a,NODE *b)
{
return min((a==NULL)?INF:a->min_,(b==NULL)?INF:b->min_);
}
NODE *qq(NODE *copy)
{
// function for copying a node into another
NODE *q=&nr[nw++];
if(copy==NULL)
return q;
q->one=copy->one;
q->zero=copy->zero;
q->min_=copy->min_;
return q;
}
ll traverse(NODE *ptr,ll idx,ll tight,ll req,ll val)
{
// req is weight W from query of type 2 and val is xor weight X for node.
if(ptr==NULL)
return INF;
if(!tight)
{
return ptr->min_;
}
if(idx<0)
{
return ptr->min_;
}
if(req&(1<<idx))
{
if(val&(1<<idx))
{
ll a=traverse(ptr->zero,idx-1,1,req,val);
ll b=traverse(ptr->one,idx-1,0,req,val);
return min(a,b);
}
else
{
ll a=traverse(ptr->zero,idx-1,0,req,val);
ll b=traverse(ptr->one,idx-1,1,req,val);
return min(a,b);
}
}
else
{
if(val&(1<<idx))
return traverse(ptr->one,idx-1,1,req,val);
else
return traverse(ptr->zero,idx-1,1,req,val);
}
}