PROBLEM LINK:
DIFFICULTY:
EASY-MEDIUM
PREREQUISITES:
Sliding Window, Greedy, Binary search
PROBLEM:
Given array A consisting of N integers. A subsequence s is an x-insider if s_i < x < s_{i+1} or s_i > x > s_{i+1} for all valid i.
For each k\in\{2,3,\dots,N\}, calculate the smallest and largest integers m such that a m-insider subsequence of A, of length k exists.
EXPLANATION:
Claim: For every k, m_k equals A_i+1 or A_i-1 for some valid i. Similarly, M_K=A_i\pm1 for some valid i.
Proof
Let s be some m_k-insider subsequence of A of length k.
Now, assume m_k \ne A_i\pm 1 for all i.
Then, s_j+1< m_k < s_{j+1}-1 or s_j+1>m_k>s_{j+1}-1 for all valid j. It directly follows that s_j < m_k-1 < s_{j+1} or s_j > m_k-1 > s_{j+1} for all valid j.
Thus, s is also an (m_k-1)-insider subsequence, breaking the minimality definition of m_k (since we’ve found a smaller m_k such that an m_k-insider subsequence exists).
A similar proof can be derived for M_K.
Now, if we instead computed for each x=A_i\pm1, the length of the longest x-insider subsequence of A, we could then derive the required solution (arrays m and M) efficiently.
How do we derive the required solution?
If s is an x-insider subsequence, then all subarrays of s are also x-insider subsequences of A. Thus, if l is the length of the longest x-insider subsequence of A, an x-insider subsequence of A, with length 2,3,\dots,l also exists.
Then, it becomes evident that the value of m_k/M_k is equal to the smallest/largest x such that the length of the longest x-insider subsequence of A is \ge k.
If we let c_i/C_i represent the smallest/largest x such that the length of the longest x-insider subsequence is exactly k, then:
- m_i=\min(c_i,c_{i+1},c_{i+2},\dots)
- M_i=\min(C_i,C_{i+1},C_{i+2},\dots)
Computing this can be done efficiently using suffix minimum/maximum!
First, let’s start by cleaning the array A. Erase all A_i where
- A_{i-1}<A_i<A_{i+1}, or
- A_{i-1}>A_i>A_{i+1}, or
- A_{i-1}=A_i.
Why?
Every element of A that we erase is guaranteed to not be required in constructing a longest length insider subsequence.
Look at the first case for example - A_{i-1}<A_i<A_{i+1}. By the definition of the problem, it is clear that no insider subsequence uses all three of the elements. Now, any subsequence s that uses A_i could be changed to use A_{i-1} or A_{i+1} instead (depending on whether A_i in s is lesser than or greater than it’s adjacent elements, respectively).
Similarly, we may show the validity of the other two cases as well.
With that done, A now looks like like a (3 year olds) representation of a rugged mountain - each element is either greater than or lesser than both of its adjacent elements (that is, A_{i-1}<A_i>A_{i+1} or A_{i-1}>A_i<A_{i+1} for every valid i).
Visualisation+Intuition for the next step
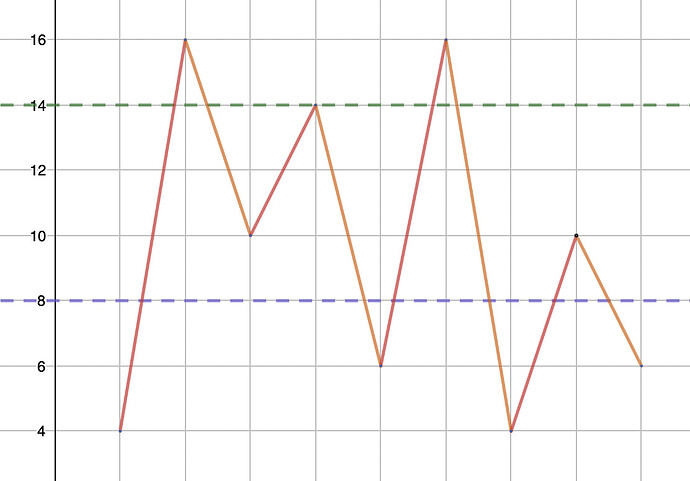
Let’s take for example, say A=[4,16,10,14,6,16,4,10,6]. Try finding the length of the longest subsequence that is an y-insider, for y=8,14.
The endpoints of the mountain like structure represents the elements of A. The green and purple lines represent y=14 and 8 respectively.
Now, a subsequence is a y-insider only if the corresponding horizontal line is strictly intersects all the edges of the mountain formed by selecting those elements.
A bit of extrapolation/educated deduction would show that the length of the longest y-insider subsequence is equal to - the number of edges of the mountain the corresponding horizontal line strictly intersects, plus 1.
Going back to our example, the number of edges the line y=14 strictly intersects equals 4. The longest y-insider subsequence is [4,16,10,16,4] whose length is 5=4+1.
Similarly the number of edges strictly intersected by y=8 equals 6. The longest y-insider subsequence is [4,16,6,16,4,10,6] whose length is 7=6+1.
Claim: The length of the longest x-insider subsequence equals 1 plus the number of valid i such that A_i<x<A_{i+1} or A_i>x>A_{i+1}.
(The proof of this is mundane and left to the reader as an exercise. Use the visualisation in the spoiler above to guide your proof).
Now, all we are left to do is compute this value for each x=A_i\pm1. Iterating over A for each x to calculate the answer would take a total of O(N^2) over all x. We can instead, for each valid i, add 1 to all x that lies strictly between A_i and A_{i+1}.
This can be done efficiently by sorting all x in non-decreasing order and using the difference array technique to update the values in linear time!
Implementation
Start by cleaning the array A, as mentioned previously.
Make an array B, comprising of all x=A_i\pm1. Sort this array in non-decreasing order. Also maintain a sliding window array mp of size |B|, where mp_i represents the length of the longest B_i-insider subsequence of A.
Iterate over A. Let the current index be i.
Use upper_bound/lower_bound to find the range of indices j such that B_j lies strictly between A_i and A_{i+1}. Increment this range in mp by 1.
Computing m and M is described about the start of the editorial. Restating very briefly, set
- c_i=\min(B_j)\forall j,\text{ where } mp_j=i
- C_i=\max(B_j)\forall j,\text{ where } mp_j=i
Then,
- m_i=\min(c_i,c_{i+1},c_{i+2},\dots)
- M_i=\min(C_i,C_{i+1},C_{i+2},\dots)
can be computed efficiently using suffix minimum/maximum.
TIME COMPLEXITY:
Cleaning array A takes O(N). Computing and sorting array B takes O(N\log N).
Finding the range of the sliding window to be updated, using lower_bound/upper_bound takes O(N\log N) over all i.
Finally, computing the arrays m and M takes O(N).
The total time complexity is therefore
per test case.
SOLUTIONS:
Editorialist’s solution can be found here
Experimental: For evaluation purposes, please rate the editorial (1 being poor and 5 excellent)
- 1
- 2
- 3
- 4
- 5
0 voters