The thing is they keep doing this no one would get anything.Which contradicts that they have to maximize the gold.
However, using the same logic we can conclude that as long as there are at least two nonempty mines, Chefu can ensure that he is always in a different mine than Chef by moving as soon as Chef moves into his mine.
I don’t understand why this invalidates anything. Let’s say Chef is “behind” Chefu’s movements by some tiny amount of time. By “tiny”, we mean “infinitesimal”, that is, Chef actually isn’t behind at all because everything is instantaneous. So even if it’s somehow optimal for Chefu to try to “escape” Chef, Chef can still manipulate his trailing of Chefu so he spends the same amount of time in each mine as Chefu.
How do you prove that no one will get anything? And how does that work when the total sum is constant?
moves are always instantaneous
What I mean by that sentence is that if there is some time t_1 and t_2 such that t_1 < t_2, Chef is in mine i and Chefu is in mine j where i \neq j during the entirety of the time interval between t_1 and t_2, then the outcome would be different than X and Y.
but that won’t be happening if they are tailing each other.
Yes, I kind of agree with you .I think if we can provide an example test case then we can be sure that this is not optimal
Agreed !!
Let c be the change in the outcome you’re talking about, then \lim\limits_{(t_2 - t_1) \to 0}{c} = 0. So because of continuity, this makes no difference. The "entirety of the time interval between t_1 and t_2" is nothing.
That seems to make a bit of sense, but it still feels very wrong for me.
I don’t really like it either, to be honest. But I believe one could craft a strong (probably calculus-based) proof for how the continuity doesn’t make a difference. I’m just not the right person to do it.
So I’m thinking that if Chef and Chefu has some “reaction time” r, then as r tends to 0 the maximum difference between the time Chef spends in a mine and the time Chefu spends in a mine will approach 0. So we know that a limit for the outcome as the reaction time tends to 0 exists. But then that doesn’t seem to necessarily indicate that there is a defined outcome when r = 0.
But can’t we apply the same limit argument to show that there is a defined outcome? Any advantage Chefu will get by evading Chef will be of the form c \cdot r, where c is some constant based on the input. This is definitely not indeterminate, and thus tends to 0 as r does.
edit: maybe c is more complex than a constant, as the mines deplete. But it should still be just some function of the input that doesn’t depend on r.
Okay, I agree with you that there may not be a defined outcome. To be honest, my intuition with this weird type of continuity isn’t strong enough to tell. But we also shouldn’t immediately conclude that there isn’t one, unless you can prove so or concretely prove its similarity to the bit problem (or something similar). I’m starting to doubt myself like crazy, so it definitely shouldn’t be me.
Can we get @taran_1407, @kingofnumbers, and/or @chemthan (or someone else, too) to resolve this?
I used the bit problem just to illustrate that a game where players can make instantaneous moves at any time may not have a defined outcome. I think it may be similar if we define the outcome as the total time that the bit is 1, after the game continues for some fixed amount of time. One player wants to maximize the outcome and the other player wants to minimize it. The outcome would approach half of the total time as the reaction time approaches 0, but I don’t know if it’s correct to say that the outcome is exactly half the total time when the reaction time is exactly 0.
An issue with the bit problem is that there are multiple conflicting ways to define it, too. For example, let r instead be the time that a player must spend between their own moves, rather than as a reaction. As r tends to 0, it models the same game, but the limit evaluates to 1 (because the player who starts off with the bit in their favor can always instantly counter their opponent) (1 meaning 100% of total time). And the way you choose to define r leads to the outcome being \frac{1}{2}.
the solution will still be uncertain for the second interpretation as say r be infinitesimally small dt say what if i other player changes it at T-dt time .(I am not sure tho i am having trouble properly defining this game)
I agree. But I should point out, there’s a distinct difference between a limit and an actual value. Take any function with a removable discontinuity:
(example)
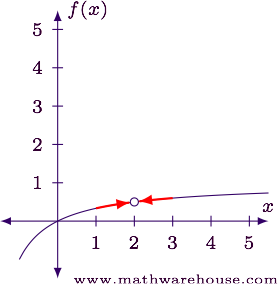
We can say \lim\limits_{x \to 2}{f(x)} = k (whatever k is), but f(x) is certainly not k - it doesn’t exist. Nonetheless, if the limit for f(x) doesn’t exist, then f(x) definitely doesn’t either (and in the bit problem’s context, it’s indeterminate).
Yeah, that’s what I meant when I said “I don’t know if it’s correct to say that the outcome is exactly half the total time when the reaction time is exactly 0.” Maybe there’s some other way to make sense of it, but the limit isn’t a rigorous proof.
What if we frame it this way for any time interval dt chef will have to choose a set of mines he works in that period and since both players are rational no matter what set chef chooses chefina can always choose the same due to each player know what other player will do.
Many people just wrote the solution for n=1, and submitted and got 100 points, without even thinking the details. This was the reason why there were a huge number of submissions on the problem. Many people wasted their time on this problem. 