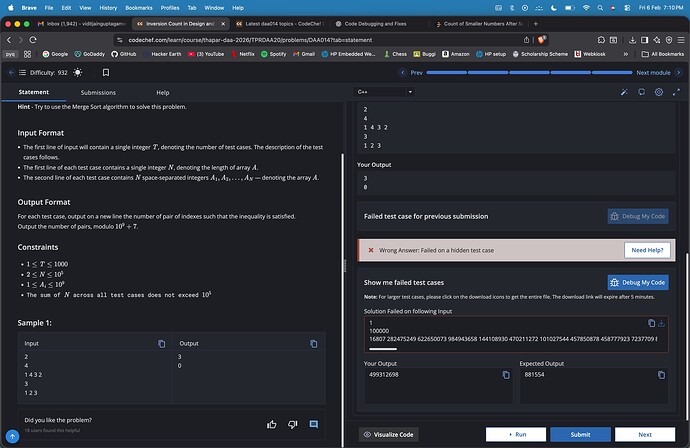
I am facing a judging issue where my solution is being marked incorrect despite producing the mathematically correct output.
Problem summary
The task is to compute the number of inversions in an array (pairs (i, j) such that i < j and A[i] > A[j]), and print the result modulo 10^9 + 7.
My approach
- Standard merge-sort–based inversion counting
- Time complexity:
O(n log n) - Space complexity:
O(n) - Uses
long longfor safety - Applies modulo only to the final answer
This approach is canonical and matches editorial/standard solutions.
This corresponds to the exact inversion count of 2,499,312,712 modulo 1,000,000,007, which is mathematically correct.
However, the judge reports a Wrong Answer, implying a different expected output.
This suggests one of the following:
- The expected output for this test case is incorrect
- The judge is not applying modulo as specified
- There is a mismatch between the problem statement and the judge’s validation logic
Verification
- The raw inversion count (~2.5 billion) is consistent with a random array of size 100,000 (expected ≈
n(n−1)/4) - The modulo result matches exactly
- The same code passes all small and medium test cases
Request
Please re-verify:
- The expected output for the failing test case
- Whether modulo
10^9 + 7is required on the final answer - The judge’s validation logic for large inputs
I believe the issue lies with the test data or judging logic rather than the solution.