PROBLEM LINK:
Author: Abhinav Jain
Tester: Hanlin Ren
Editorialist: Hanlin Ren
DIFFICULTY:
HARD
PREREQUISITES:
DP, Math, FFT
PROBLEM:
We have an N\times M matrix initially filled with zeroes, and we want to perform Q operations. In each operation, we choose some grid (x,y) and add 1 to every cell in row x and every cell in column y. (Cell (x,y) is added twice.) Find the number of ways to perform Q operations such that after these operations, there are exactly Z odd numbers in the matrix.
QUICK EXPLANATION:
- Let DP(N,Q,r) be the number of length-q sequences where every element is in \{1,2,\dots,N\}, and there are exactly r elements in \{1,2,\dots,N\} that appears an odd number of times.
- \displaystyle DP(N,Q,r)=\binom{N}{r}2^{-N}\cdot \sum_{i=0}^N\sum_{j=0}^{\min(i,r)}(-1)^j\binom{r}{j}\binom{N-r}{i-j}(N-2i)^Q.
- Given N,Q,r, we can compute DP(N,Q,r) in O(N\log N) time in FFT.
- We enumerate all 0\le i\le N,0\le j\le M, if iM+jN-2ij=Z, we add f(N,Q,i)\cdot f(M,Q,j) into the answer.
- We need to deal with the special case where Z=MN/2.
- Time complexity: O(Y\cdot N\log N), where Y is the number of pairs (r,c) such that rM+cN-2rc=Z.
It seems that many contestants use O(N^2) or even O(N\log N) algorithms, which is even faster than the intended solution! Please share your approaches with us.
EXPLANATION:
First, we decompose each operation (x,y) as two operations: adding 1 to the x-th row (a row operation) and adding 1 to the y-th column (a column operation). Let r be the number of rows operated an odd number of times, and c be the number of columns operated an odd number of times. (We’ll call such rows and columns odd.) Then we should have Z=r(M-c)+c(N-r). (For the derivation of this formula, please refer to the editorial for SAKTAN).
Subtask 1
Let’s enumerate r and c. If Z=r(M-c)+c(N-r), we compute the number of operation sequences such that there are r odd rows and c odd columns, and add the result in our answer. Since the row operations and column operations are independent, we only need to
- find the number of sequences of row operations with r odd rows,
- do the same for sequences of column operations with c odd columns, and
- multiply the two results together.
Now let’s focus on rows. What we want to find is actually the number of length-Q sequences A_1,A_2,\dots,A_Q such that:
- each A_i is an integer in [1,N];
- Among [1,N], there are exactly r numbers that appear in the sequence an odd number of times.
(A_i is the index of the row/column that we perform operations on.)
Let DP(N,Q,r) be the number of such sequences. We can compute DP(N,Q,r) in O(NQ) time by the following formula:
\displaystyle DP(N,Q,r)=(N-r+1)\cdot DP(N,Q-1,r-1)+(r+1)\cdot DP(N,Q-1,r+1),
where edge case is DP(0,0,0)=1.
Explanation: consider a sequence A_1,A_2,\dots,A_Q.
- Suppose A_Q appears an even number of times in the prefix A_1,A_2,\dots,A_{Q-1}. Then for the prefix A_1,A_2,\dots,A_{Q-1}, there are r-1 elements in [1,N] that appears an odd number of times. So there are DP(N,Q-1,r-1) ways to choose this prefix, and then N-r+1 ways to choose the number A_Q.
- Suppose A_Q appears an odd number of times in the prefix A_1,A_2,\dots,A_{Q-1}. Then for the prefix A_1,A_2,\dots,A_{Q-1}, there are r+1 elements in [1,N] that appears an odd number of times. So there are DP(N,Q-1,r+1) ways to choose this prefix, and then r+1 ways to choose the number A_Q.
The time complexity is O(NQ) for each pair of (r,c). In the end of this editorial, we’ll estimate the number of valid pairs of (r,c).
Derivation of DP(N,Q,r)
TL;DR:
\displaystyle DP(N,Q,r)=\binom{N}{r}2^{-N}\cdot \sum_{i=0}^N\sum_{j=0}^{\min(i,r)}(-1)^j\binom{r}{j}\binom{N-r}{i-j}(N-2i)^Q.
Admin’s derivation
Prerequisites: exponential generating functions.
Admin's derivation
Let’s treat DP(N,Q,r) as a function of Q, and define its exponential generating function (EGF) as
\displaystyle dp_{N,r}(x)=\sum_{Q=0}^{+\infty}\frac{x^Q}{Q!}DP(N,Q,r).
As a start, we also define two functions:
- F_{N,Q}=DP(N,Q,0) is the number of length-Q sequences such that every element is in [1,N] and every x\in[1,N] appears an even number of times;
- G_{N,Q}=DP(N,Q,N) is the number of length-Q sequences such that every element is in [1,N] and every x\in[1,N] appears an odd number of times.
We define their EGF as f_N(x)=\sum_{Q=0}^{+\infty}\frac{x^Q}{Q!}F_{N,Q} and g_N(x)=\sum_{Q=0}^{+\infty}\frac{x^Q}{Q!}G_{N,Q}. By the properties of EGF,
\displaystyle dp_{N,r}(x)=\binom{N}{r}f_{N-r}(x)g_r(x).
proof
To pick a sequence where r elements in [1,N] appears an odd number of times, we can
- First, pick r elements from [1,N]; (We have \binom{N}{r} choices)
- Pick a sequence of length i(0\le i\le Q) over these r elements, such that every element appears an odd number of times; (We have G_{r,i} choices)
- Pick a sequence of length Q-i over the rest N-r elements, such that ever element appears an even number of times; (We have F_{N-r,Q-i} choices)
- Interleave these two sequences. (We have \binom{Q}{i} choices)
Therefore
\displaystyle DP(N,Q,r)=\binom{N}{r}\sum_{i=0}^QG_{r,i}F_{N-r,Q-i}\binom{Q}{i}.
Substitute this into EGF:
\displaystyle dp_{N,r}(x)=\sum_{Q=0}^{+\infty}DP(N,Q,r)\frac{x^Q}{Q!}
\displaystyle dp_{N,r}(x)=\sum_{Q=0}^{+\infty}\binom{N}{r}\sum_{i=0}^QG_{r,i}F_{N-r,Q-i}\binom{Q}{i}\frac{x^Q}{Q!}
expand \binom{Q}{i} and x^Q:
\displaystyle dp_{N,r}(x)=\sum_{Q=0}^{+\infty}\binom{N}{r}\sum_{i=0}^QG_{r,i}F_{N-r,Q-i}\frac{Q!}{i!(Q-i)!}\frac{x^i\cdot x^{Q-i}}{Q!}
Group the products:
\displaystyle dp_{N,r}(x)=\sum_{Q=0}^{+\infty}\binom{N}{r}\sum_{i=0}^QG_{r,i}\frac{x^i}{i!}\cdot F_{N-r,Q-i}\frac{x^{Q-i}}{(Q-i)!}
Let j=Q-i:
\displaystyle dp_{N,r}(x)=\binom{N}{r}\sum_{i=0}^{+\infty}\sum_{j=0}^{+\infty}G_{r,i}\frac{x^i}{i!}\cdot F_{N-r,j}\frac{x^j}{j!}
That is, dp_{N,r}(x)=\binom{N}{r}g_r(x)f_{N-r}(x). QED.
Now we need to find f_N(x) and g_N(x). By properties of EGF, we have f_N(x)=f_1(x)^N and g_N(x)=g_1(x)^N.
proof
The proof method is very similar to the above proof. You should try it yourself. Hint: prove f_N(x)=f_{N-1}(x)f_1(x).
We also have f_1(x)=\frac{1}{2}(e^x+e^{-x}), g_1(x)=\frac{1}{2}(e^x-e^{-x}).
proof
We need the identity
\displaystyle e^x=\sum_{i=0}^{+\infty}\frac{x^i}{i!}=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\dots.
By definition, f_{1,r}=1 if r is even, and f_{1,r}=0 if r is odd. Therefore
\displaystyle f_1(x)=\sum_{i=0}^{+\infty}\frac{x^{2i}}{(2i)!}=1+\frac{x^2}{2!}+\frac{x^4}{4!}+\dots.
We note that
\displaystyle e^{-x}=\sum_{i=0}^{+\infty}\frac{(-x)^i}{i!}=1-x+\frac{x^2}{2!}-\frac{x^3}{3!}+\dots,
so it’s easy to see from the above equations that f_1(x)=\frac{1}{2}(e^x+e^{-x}).
Note that
\displaystyle g_1(x)=\sum_{i=0}^{+\infty}\frac{x^{2i+1}}{(2i+1)!}=x+\frac{x^3}{3!}+\frac{x^5}{5!}\dots.
The argument for g_1(x) is essentially the same. QED.
Now we can compute dp_{N,r}(x) as follows:
\displaystyle dp_{N,r}(x)=\binom{N}{r}f_{N-r}(x)g_r(x)
\displaystyle dp_{N,r}(x)=\binom{N}{r}2^{-N}(e^x+e^{-x})^{N-r}(e^x-e^{-x})^r
Using the Binomial theorem, we have
\displaystyle dp_{N,r}(x)=\binom{N}{r}2^{-N}\left(\sum_{j=0}^{N-r}\binom{N-r}{j}e^{jx}e^{-(N-r-j)x}\right)\cdot\left(\sum_{k=0}^r\binom{r}{k}e^{kx}e^{-(r-k)x}(-1)^{r-k}\right).
\displaystyle dp_{N,r}(x)=\binom{N}{r}2^{-N}\sum_{j=0}^{N-r}\sum_{k=0}^r\binom{N-r}{j}\binom{r}{k}(e^x)^{2j+2k-N}(-1)^{r-k}.
Let’s “extract” the coefficient of x^Q of dp_{N,r}(x):
\displaystyle dp_{N,r}(x)=\binom{N}{r}2^{-N}\sum_{j=0}^{N-r}\sum_{k=0}^r\binom{N-r}{j}\binom{r}{k}\sum_{Q=0}^{+\infty}(2j+2k-N)^Q\frac{x^Q}{Q!}(-1)^{r-k}
Recall that
\displaystyle dp_{N,r}(x)=\sum_{n=0}^{+\infty}DP(N,Q,r)\frac{x^Q}{Q!}
Therefore
\displaystyle DP(N,Q,r)=\binom{N}{r}2^{-N}\sum_{j=0}^{N-r}\sum_{k=0}^r\binom{N-r}{j}\binom{r}{k}(2j+2k-N)^Q(-1)^{r-k}.
This is equivalent to the claim of formula DP(N,Q,r) at “TL;DR” section.
Tester’s derivation
(Personally I think this derivation is a bit complicated, but I like it very much. I hope you enjoy reading it.)
Prerequisites: linear algebra, in particular diagonalization of matrices
Tester's derivation
First, we observe that DP(N,Q,0) is the number of length-Q closed walks from (0,0,\dots,0) in a hypercube graph of order N. The hypercube graph is defined as follows:
- There are 2^N vertices, each vertex corresponds to a length-N vector that only contains 0 and 1.
- For every two vertices \vec{v}_1 and \vec{v}_2, if they differ by exactly one coordinate (i.e. their Hamming distance is 1), the there is an edge between them.
An example of a hypercube graph of order 3:
Consider a sequence (A_1,A_2,\dots,A_Q) where each number in [1,N] appears an even number of times. By definition, the number of such sequences is exactly DP(N,Q,0). Now for a particular sequence A, we define a walk in the hypercube graph as follows: the i-th vertex we pass through is (b_{i1},b_{i2},\dots,b_{iN}), where b_{ij} is 1 if and only if j appears an odd number of times in (A_1,A_2,\dots,A_i). Intuitively, when we add an element A_{i+1}, we walk along the “A_{i+1}-th dimension” of the hypercube. The generated walk is a closed walk of Q steps, from (0,0,\dots,0) to the same vertex (0,0,\dots,0).
An example
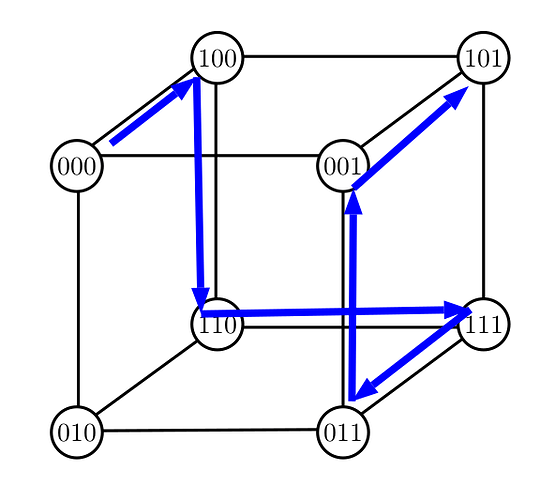
For example, when N=3, consider the sequence (1,3,3,3,1,3). Every element in [1,N] appears an even number of times. The vertices in the walk are:
vertex | current element
(0,0,0) | None
(1,0,0) | 1
(1,0,1) | 3
(1,0,0) | 3
(1,0,1) | 3
(0,0,1) | 1
(0,0,0) | 3
and it corresponds to the following walk:
The above transformation from valid sequences to closed walks is actually a bijection. Thus DP(N,Q,0) is exactly the number of Q-step closed walks starting at (0,0,\dots,0).
We can generalize this result: DP(N,Q,r) is the sum of the number of Q-step walks from (0,0,\dots,0) to \vec{x}, where the sum is taken over all \vec{x}'s with exactly r ones (i.e. Hamming weight r). The reason is simple: if there are exactly r numbers in [1,N] that appears an odd number of times in (A_1,A_2,\dots,A_Q), then the above walk algorithm should stop at some \vec{x} that contains r ones. Moreover, the coordinates of ones are exactly the elements in [1,N] that appeared an odd number of times.
Another example
Let’s still think of N=3. Consider the sequence (1,2,3,1,2,1). The walk should end at (1,0,1) since elements 1 and 3 appears an odd number of times, but 2 appears an even number of times. The vertices in the walk are:
vertex | current element
(0,0,0) | None
(1,0,0) | 1
(1,1,0) | 2
(1,1,1) | 3
(0,1,1) | 1
(0,0,1) | 2
(1,0,1) | 1
and it corresponds to the following walk:
Let cnt_r be the number of Q-step walks from (0,0,0,\dots,0) to (\underbrace{1,1,\dots,1}_{r\text{ ones}},0,0,\dots,0), then DP(N,Q,r)=cnt_r\cdot \binom{N}{r}. This is because there are \binom{N}{r} vertices that has Hamming weight r, and they’re equivalent.
Now we want to find the number of length-Q walks from a certain vertex \vec{s}=(0,0,\dots,0) to a certain vertex \vec{t}=(\underbrace{1,1,\dots,1}_{r\text{ ones}},0,0,\dots,0) in the hypercube graph. Let A be the adjacency matrix of the hypercube graph, then we need to find the (s,t)-th entry of A^Q.
An example
Still think of N=3. Here the adjacency matrix is
A=\begin{pmatrix}
&{\tiny 000}&{\tiny 001}&{\tiny 010}&{\tiny 011}&{\tiny 100}&{\tiny 101}&{\tiny 110}&{\tiny 111}\\
{\tiny 000}&0&1&1&0&1&0&0&0\\
{\tiny 001}&1&0&0&1&0&1&0&0\\
{\tiny 010}&1&0&0&1&0&0&1&0\\
{\tiny 011}&0&1&1&0&0&0&0&1\\
{\tiny 100}&1&0&0&0&0&1&1&0\\
{\tiny 101}&0&1&0&0&1&0&0&1\\
{\tiny 110}&0&0&1&0&1&0&0&1\\
{\tiny 111}&0&0&0&1&0&1&1&0\\
\end{pmatrix}
If we want to find length-2 paths, we should calculate A^2
A^2=\begin{pmatrix}
&{\tiny 000}&{\tiny 001}&{\tiny 010}&{\tiny 011}&{\tiny 100}&{\tiny 101}&{\tiny 110}&{\tiny 111}\\
{\tiny 000}&3&0&0&2&0&2&2&0\\
{\tiny 001}&0&3&2&0&2&0&0&2\\
{\tiny 010}&0&2&3&0&2&0&0&2\\
{\tiny 011}&2&0&0&3&0&2&2&0\\
{\tiny 100}&0&2&2&0&3&0&0&2\\
{\tiny 101}&2&0&0&2&0&3&2&0\\
{\tiny 110}&2&0&0&2&0&2&3&0\\
{\tiny 111}&0&2&2&0&2&0&0&3\\
\end{pmatrix}.
One can check that (A^2)_{uv} is indeed the number of length-2 walks from u to v. E.g. if u=v, then (A^2)_{uv}=3, which corresponds to the three neighbors of u. You can always walk from u to one of its neighbors, and then immediately come back to u.
The point is that A is diagonalizable, and its decomposition has a closed form. Let’s label the indices of A by length-n Boolean sequences, and introduce the following notations:
- |u| is the number of 1's in the vector u. e.g. |(1,0,0,1,0)|=2.
- u\& v denotes pairwise AND. *e.g. (1,0,1,0)\&(1,1,0,0)=(1,0,0,0).
It can be seen here that if A is the adjacency matrix of the hypercube graph with 2^N vertices, then A=PDP^{-1}, where
\displaystyle D_{u,v}=\begin{cases}0&u\ne v\\N-2|u|&u=v\end{cases}
\displaystyle P_{u,v}=\begin{cases}-1/\sqrt{2^N}&|u\&v|\text{ is odd}\\1/\sqrt{2^N}&|u\&v|\text{ is even}\end{cases}
and P^{-1}=P.
An example
Yes let’s still play with the case that N=3. Here we have
D=\begin{pmatrix}
&{\tiny 000}&{\tiny 001}&{\tiny 010}&{\tiny 011}&{\tiny 100}&{\tiny 101}&{\tiny 110}&{\tiny 111}\\
{\tiny 000}&3&0&0&0&0&0&0&0\\
{\tiny 001}&0&1&0&0&0&0&0&0\\
{\tiny 010}&0&0&1&0&0&0&0&0\\
{\tiny 011}&0&0&0&-1&0&0&0&0\\
{\tiny 100}&0&0&0&0&1&0&0&0\\
{\tiny 101}&0&0&0&0&0&-1&0&0\\
{\tiny 110}&0&0&0&0&0&0&-1&0\\
{\tiny 111}&0&0&0&0&0&0&0&-3\\
\end{pmatrix}
P=\frac{1}{\sqrt{8}}\begin{pmatrix}
&{\tiny 000}&{\tiny 001}&{\tiny 010}&{\tiny 011}&{\tiny 100}&{\tiny 101}&{\tiny 110}&{\tiny 111}\\
{\tiny 000}&1&1&1&1&1&1&1&1\\
{\tiny 001}&1&-1&1&-1&1&-1&1&-1\\
{\tiny 010}&1&1&-1&-1&1&1&-1&-1\\
{\tiny 011}&1&-1&-1&1&1&-1&-1&1\\
{\tiny 100}&1&1&1&1&-1&-1&-1&-1\\
{\tiny 101}&1&-1&1&-1&-1&1&-1&1\\
{\tiny 110}&1&1&-1&-1&-1&-1&1&1\\
{\tiny 111}&1&-1&-1&1&-1&1&1&-1\\
\end{pmatrix}
You can verify that P^2=I (i.e. P=P^{-1}) and PDP=A.
Then we have
\displaystyle A^Q=(PDP^{-1})^Q=\underbrace{PDP^{-1}\cdot PDP^{-1}\cdot\dots\cdot PDP^{-1}}_{Q\text{ times}}=PD^QP^{-1}.
It translates to
\displaystyle A^Q_{0,u}=\sum_vP_{0,v}D_{v,v}^QP_{v,u}=\frac{1}{2^N}\sum_v(N-2|v|)^Q(-1)^{|u\& v|}.
Recall that DP(N,Q,r)=\binom{N}{r}A^Q_{0,u} where u contains r ones.
There are 2^N summands in the above formula (one for each v). We still need to solve it faster.
We enumerate j=|u\&v| and k=|v|-|u\&v|. The number of v that satisfies both condition on j and k is \binom{|u|}{j}\binom{n-|u|}{k}: we independently choose j ones from the indices which are 1 in u, and choose k ones from the other indices. Substitute it back, we obtain
\displaystyle DP(N,Q,r)=\binom{N}{r}2^{-N}\sum_{j=0}^r\sum_{k=0}^{N-r}\binom{r}{j}\binom{n-r}{k}(N-2j-2k)^Q(-1)^j.
This is also equivalent to the claim of formula DP(N,Q,r) at “TL;DR” section.
Remark. I think we can also derive this formula directly from the transition matrix corresponding to DP equation. However I didn’t find the patterns of the eigenvectors (i.e. matrix P in A=PDP^{-1}) in the first glance. (I guess it can be done with more work.)
Using FFT
Recall the formula
\displaystyle DP(N,Q,r)=\binom{N}{r}2^{-N}\cdot \sum_{i=0}^N\sum_{j=0}^{\min(i,r)}(-1)^j\binom{r}{j}\binom{N-r}{i-j}(N-2i)^Q.
The most straightforward implementation takes O(N^2) time to compute a single value of DP(N,Q,r). However, it’s easy to see that the above can be written in the form of convolution, and solved by FFT in O(N\log N) time:
- Let’s find the convolution of two sequences \{(-1)^j\binom{r}{j}\}_{j=0}^r and \{\binom{N-r}{k}\}_{k=0}^{N-r}. Let the result be sequence \{C_i\}.
- C_i=\sum_{j=0}^i(-1)^j\binom{r}{j}\binom{N-r}{i-j}.
- Given \{C_i\}, we can then compute DP(N,Q,r) easily.
Estimating the number of valid (r,c)'s
Recall that we compute DP(N,Q,r) and DP(M,Q,c) for each pair (r,c) such that r(M-c)+c(N-r)=Z. Of course we want to know the number of pairs (r,c) that satisfies the above condition.
Suppose r(M-c)+c(N-r)=Z. Then we have (2r-N)(2c-M)=4rc-2rM-2cN+MN=MN-2Z. It follows that 2r-N and 2c-M must be divisors of MN-2Z. So there are two cases:
- If MN\ne 2Z, then the constraints says |MN-2Z|\le 4\times 10^6. Every number below this bound has at most 384 divisors (including negative ones), so this is an upper bound of the number of (r,c) pairs. Actually, since 2r-N and 2c-M should be in the range [-N,N] and [-M,M] respectively, the above bound is not tight. We can run an experiment (for M=N=2,000) to show that the number of valid (r,c)'s is at most 140.
- If MN=2Z, then there may be a lot of (r,c)'s since every number divides 0. More precisely, the pair (r,c) is valid if and only if either 2r=N or 2c=M. In this case:
- At least one of N,M is even;
- If N is even and M is odd, then r=N/2 and c can be any number. The answer is DP(N,Q,N/2)\cdot M^Q (since column operations are arbitrary).
- If N is odd and M is even, then c=N/2 and r can be any number. Similarly the answer is DP(M,Q,M/2)\cdot N^Q.
- If both N and M are even, then
- The contribution of pairs with r=N/2 to the answer is DP(N,Q,N/2)\cdot M^Q;
- The contribution of pairs with c=M/2 to the answer is DP(M,Q,M/2)\cdot N^Q;
- The contribution of pair (N/2,M/2) is DP(N,Q,N/2)\cdot DP(M,Q,M/2). Since it’s calculated twice, we need to subtract it from the answer.
- Therefore by the inclusion-exclusion principle, the answer is DP(N,Q,N/2)\cdot M^Q+DP(M,Q,M/2)\cdot N^Q-DP(N,Q,N/2)\cdot DP(M,Q,M/2).
Summary
- We can use exponential generating functions, or matrix diagonalization, to derive the formula for DP(N,Q,r)
- We can use FFT to accelerate the computation of each DP(N,Q,r)
- If Z\ne MN/2, there are not many (r,c) pairs we need to consider, so we deal with them in a straightforward way;
- We need to deal with the special case that Z=MN/2.
ALTERNATE EXPLANATION:
It seems that many people use other approaches (that we didn’t even realize during the preparation of the problem!) which are faster than current approach. Please feel free to share your approaches!
SOLUTIONS:
Setter's Solution
#include <bits/stdc++.h>
using namespace std;
const int MX = 1 << 14, md = 998244353;
int bpow(int a, int p) {
int r = 1;
while (p > 0) {
if (p % 2 == 1) r = r * 1LL * a % md;
a = a * 1LL * a % md;
p /= 2;
}
return r;
}
namespace FFT {
const int root = 31;
int rev[MX], N = -1;
void init(int n) {
assert((n & -n) == n && n <= MX);
int log_n = 0;
while ((n >> log_n) > 1) log_n++;
for (int i = 0; i < n; i++) {
rev[i] = 0;
for (int j = 0; j < log_n; j++)
rev[i] |= (i >> j & 1) << (log_n - 1 - j);
if (rev[i] < i) rev[i] = i;
}
N = n;
}
void fft(int a[], int n, bool invert) {
assert(n == N);
static int w_pow[MX];
for (int i = 0; i < n; i++) swap(a[i], a[rev[i]]);
for (int len = 1; len < n; len *= 2) {
w_pow[0] = 1;
w_pow[1] = bpow(root, (1 << 23) / (2 * len));
if (invert) w_pow[1] = bpow(w_pow[1], md - 2);
for (int i = 2; i < len; i++) w_pow[i] = w_pow[i - 1] * 1ll * w_pow[1] % md;
for (int i = 0; i < n; i += 2 * len)
for (int j = i, k = i + len; j < i + len; j++, k++) {
int t = a[k] * 1ll * w_pow[j - i] % md, u = a[j];
a[k] = u - t < 0 ? u - t + md : u - t;
a[j] = u + t >= md ? u + t - md : u + t;
}
}
if (invert) {
int n_inv = bpow(n, md - 2);
for (int i = 0; i < n; i++) a[i] = a[i] * 1ll * n_inv % md;
}
}
}
int powQ[2 * MX + 1], C[MX + 1][MX + 1];
void precalc(int n, int q) {
for (int i = -1 * n; i <= n; i++) {
powQ[MX + i] = bpow((i + md) % md, q);
}
C[0][0] = 1;
for (int i = 1; i <= n; i++) {
C[i][0] = 1;
for (int j = 1; j <= i; j++) {
C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
C[i][j] %= md;
}
}
}
long calc(int n, int t, int q) {
int N = 1;
while (n >= N) N *= 2;
FFT::init(N);
static int a[MX], b[MX];
fill(a, a + N, 0);
fill(b, b + N, 0);
for (int k = 0; k <= t; k++) {
a[k] = C[t][k];
if ((t - k) % 2 == 1) a[k] = md - a[k];
}
for (int r = 0; r <= n - t; r++) {
b[r] = C[n - t][r];
}
FFT::fft(a, N, false);
FFT::fft(b, N, false);
for (int i = 0; i < N; i++) {
a[i] = a[i] * 1LL * b[i] % md;
}
FFT::fft(a, N, true);
long res = 0;
for (int s = 0; s <= n; s++) {
res = ( res+ a[s] * 1LL * powQ[2 * s - n + MX] % md)%md;
}
res *= C[n][t];
res %= md;
for (int i = 0; i < n; i++) {
res *= (md + 1) / 2;
res %= md;
}
return res;
}
int main() {
int T;
ignore = scanf("%d", &T);
while (T--) {
int n, m, q, z;long long int qq;
ignore = scanf("%d %d %lld %d", &n, &m, &qq, &z);
q = qq % (md - 1);
precalc(max(n, m), q);
int ans = 0;
if (2 * z == n * m) {
if (n % 2 == 0) {
ans = (ans + powQ[m + MX] * calc(n, n / 2, q)) % md;
}
if (m % 2 == 0) {
ans = (ans + powQ[n + MX] * calc(m, m / 2, q)) % md;
}
if (n % 2 == 0 && m % 2 == 0) {
ans = (ans - calc(n, n / 2, q) * calc(m, m / 2, q)) % md;
if (ans < 0) ans += md;
}
}
else {
for (int x = 0; x <= n; x++)
for (int y = 0; y <= m; y++)
if (x * (m - y) + (n - x) * y == z) {
ans = (ans + calc(n, x, q) * calc(m, y, q)) % md;
}
}
printf("%d\n", ans);
}
return 0;
}
Tester's Solution
#include <bits/stdc++.h>
using namespace std;
#define mod 998244353
typedef long long ll;
int fpm(int x, int y) {int p = 1, s = x; for (; y; y >>= 1) {if (y & 1) p = (1ll * p * s) % mod; s = (1ll * s * s) % mod;} return p;}
int tn = 4096, itn = 998000641, w = 63912897;//itn = tn ^ (-1), w = 3 ^ ((mod - 1) / tn)
void fft(int *a, int *pw){
int i, j, k, t, r;
for (i = j = 0; i < tn; i++){
if (i < j) swap(a[i], a[j]);
for (k = tn >> 1; (j ^= k) < k; k >>= 1);
}
for (i = 2, t = (tn >> 1); i <= tn; i <<= 1, t >>= 1)
for (j = 0; j < tn; j += i)
for (k = 0; k < (i >> 1); k++){
r = (1ll * a[j + k + (i >> 1)] * pw[t * k]) % mod;
a[j + k + (i >> 1)] = (a[j + k] - r + mod) % mod;
a[j + k] = (a[j + k] + r) % mod;
}
}
int pw[8200], pr[8200];
int C[3333][3333], Cf[3333][8200], Cf2[3333][8200];
bool k1[3333], k2[3333];
void init() {
C[0][0] = 1;
for (int i = 1; i <= 3000; i++) {
C[i][0] = C[i][i] = 1;
for (int j = 1; j < i; j++) C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % mod;
}
for (int i = pw[0] = pr[0] = 1; i < tn; i++) pw[i] = pr[tn - i] = (1ll * pw[i - 1] * w) % mod;
}
int pp[6333], *p = pp + 3111;
int seq1[8200];
int calc(int q, int n, int x) {
int sum = 0, tmp;
if (!k1[x]) {
k1[x] = 1;
for (int i = 0; i <= x; i++) Cf[x][i] = (1ll * C[x][i] * itn) % mod;
fft(Cf[x], pw);
}
if (!k2[n - x]) {
k2[n - x] = 1;
for (int i = 0; i <= n - x; i++) {
if (i & 1) Cf2[n - x][i] = mod - C[n - x][i];
else Cf2[n - x][i] = C[n - x][i];
}
fft(Cf2[n - x], pw);
}
for (int i = 0; i < tn; i++) seq1[i] = (1ll * Cf[x][i] * Cf2[n - x][i]) % mod;
fft(seq1, pr);
for (int i = 0; i <= n; i++)
sum = (sum + 1ll * seq1[i] * p[n - 2 * i]) % mod;
tmp = (1ll * fpm(2, mod - 1 - n) * C[n][x]) % mod;
return (1ll * tmp * sum) % mod;
}
int n, m, a, ans;
ll qq; int q;
void doit() {
cin >> n >> m >> qq >> a; ans = 0; q = qq % (mod - 1);
for (int i = -max(n, m); i <= max(n, m); i++) p[i] = fpm(mod + i, q);
if (a * 2 == n * m) {
if (~n & 1)
ans = (1ll * calc(q, n, n >> 1) * fpm(m, q) + ans) % mod;
if (~m & 1)
ans = (1ll * calc(q, m, m >> 1) * fpm(n, q) + ans) % mod;
if ((~n & 1) && (~m & 1)) {
ans = (ans - 1ll * calc(q, n, n >> 1) * calc(q, m, m >> 1)) % mod;
if (ans < 0) ans += mod;
}
} else {
for (int i = 0; i <= n; i++)
for (int j = 0; j <= m; j++)
if (i * m + j * n - 2 * i * j == a)
ans = (1ll * calc(q, n, i) * calc(q, m, j) + ans) % mod;
}
cout << ans << endl;
}
int main() {init(); int t; cin >> t; while (t--) doit(); return 0;}