PROBLEM LINK :
Practice ,
Contest
PREREQUISITES : dfs , Segment trees , dp
PROBLEM : Given a tree with edges directed towards root and nodes having some ticket information which allows you to travel k units towards the root with cost w . Answer Q queries i.e output the minimum cost for travelling from a node x to root .
OBSERVATIONS: Consider the tree to be rooted at 1 , so now every node has a directed edge towards its parent except the root , which means there is a unique path from every node to the root 1. So if we solve the problem for one unique path or one node, we can extend it for other paths as well .
EXPLANATION:
Lets try to solve the problem for a node X at depth H from the root 1 . So for now forget the tree and think of it as a 1D vector V where you have all the H-1 nodes that are between root and node X . The nodes inside the vector are sorted in the order of increasing depth . Lets just denote DP[x] to be the minimum cost of travelling from node X to the root .
So now for the given node X , lets just iterate over all the tickets present at node X and DP state will be like this :
for(int i=0;i<total_tickets;i++) // loop 1
{
K=current_ticket_jump_info;
W=weight_ticket_info;
for(int j=V.size()-1;j>= max(0,V.size()-1-k);j++) //loop 2
{
DP[X]=min( DP[X] , DP[V[j]] + W );
}
}
Code Explanation : Loop 1 simply iterates over the tickets at x and for a given ticket we can move at max K steps upwards towards the root and as we have already stored those nodes in our vector V , we can iterate over it . so the inner loop moves over those K steps to find the minimum cost .
But how can we calculate vector V for every node x ? Here comes DFS in action :
void dfs(int u,int p)
{
V.push_back(u);
for(int i=0 ; i< adj[u].size() ; i++)
{
if(adj[u][i]==p)continue;
dfs(adj[u][i],u);
}
V.pop_back();
}
Code Explanation : what we are doing over here is pushing a node u to the vector V when we haven’t discovered the subtree of u and pop it when the whole subtree is discovered . Its obvious that u will always lie between the path of any node which is in subtree of u and root . And this also take cares of the sorted depth order . If you aren’t getting this , try to draw a few trees .
So the final code :
void dfs(int u,int p)
{
V.push_back(u);
for(int l=0 ; l< adj[u].size() ; l++)
{
if(adj[u][l]==p)continue;
int x =adj[u][l];
for(int i=0;i<total_tickets;i++) // loop 1
{
K=current_ticket_jump_info;
W=weight_ticket_info;
for(int j=V.size()-1;j>= max(0,V.size()-1-k);j++) //loop 2
{
DP[x]=min( DP[x] , DP[V[j]] + W );
}
}
dfs(adj[u][l],u);
}
V.pop_back();
}
Complexity: : Well the complexity is simply O(N+M*N) , Damn ![]() ! we need optimisations
! we need optimisations ![]()
OBSERVATIONS: if we look at the inner loop of the code which goes up to K times and we find the minimum of DP , this can be done using any data structure that supports RMQ + Point updates in O(logn) time . Which will make the total complexity to be O(N + MlogN) and that is cool ![]() .
.
So what we can do is build a segment tree that supports two operations . First : find the minimum element in range L,R and Second: update an element’s value to VAL. And obviously as we need to query for the minimum element between [H-K , H] so we will build the tree over height H .
//consider segment tree has already been built with every element to be infinity apart from element 1 , which will be 0 because at height 1 , root is present .
void dfs(int u,int p,int h)
{
updatetree(0,1,n,h,DP[u]); // update the tree element at position h with its DP value . remember , node u is at height h and tree is built on height so we will update h position in the tree and not u .
for(int l=0 ; l< adj[u].size() ; l++)
{
if(adj[u][l]==p)continue;
int x =adj[u][l];
for(int i=0;i<total_tickets;i++) // loop 1
{
K=current_ticket_jump_info;
W=weight_ticket_info;
DP[x]=query(0,1,n,max(1,h-K),h)+W;
}
dfs(adj[u][l],u,h+1);
}
updatetree(0,1,n,h,INFINITY); // update the tree at with element h with Infinity as we are done with its subtree .
}
Now just print DP[x] for every query . AC ![]() . For the actual code refer this .
. For the actual code refer this .
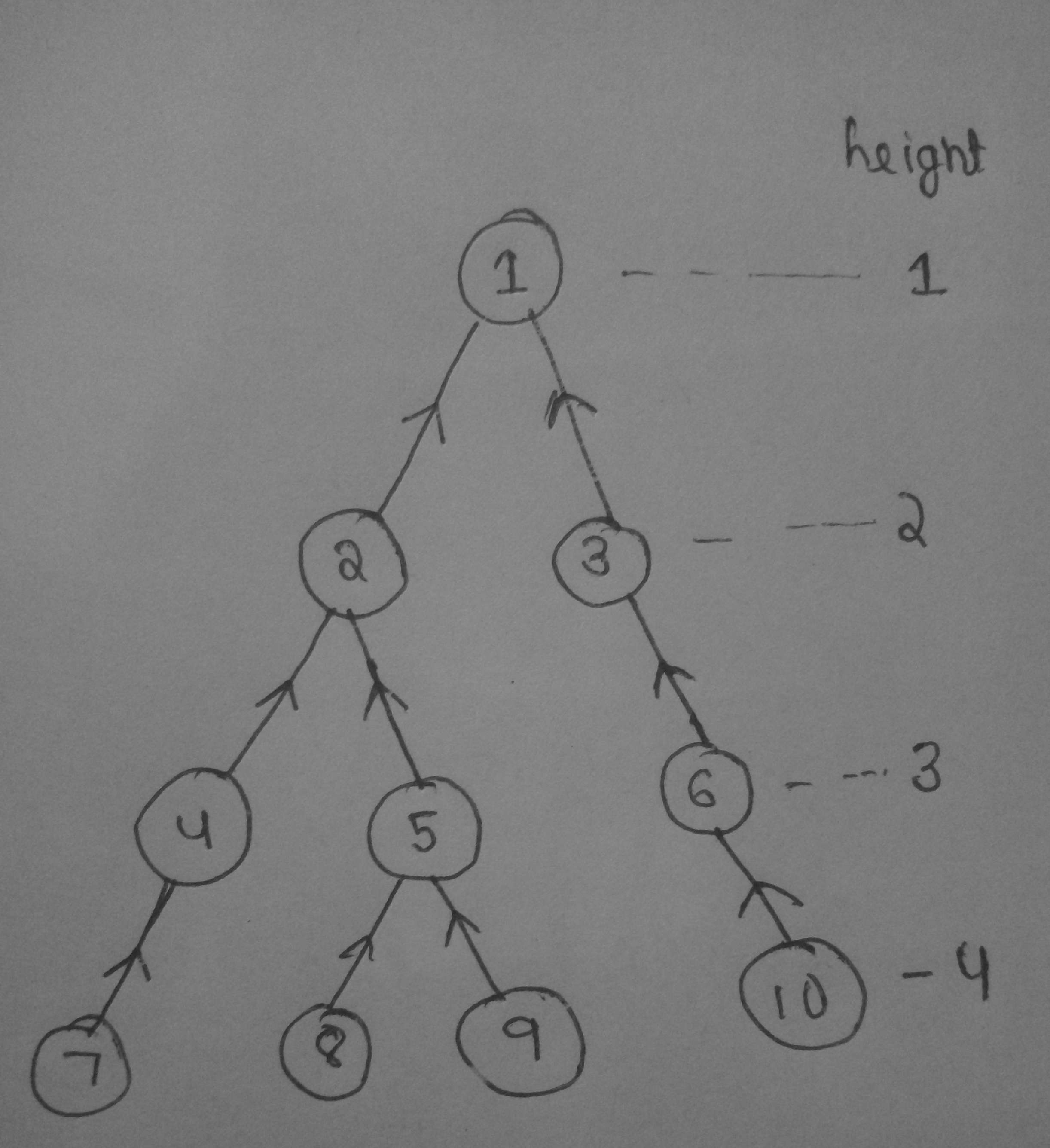
For example :
This is the given tree .
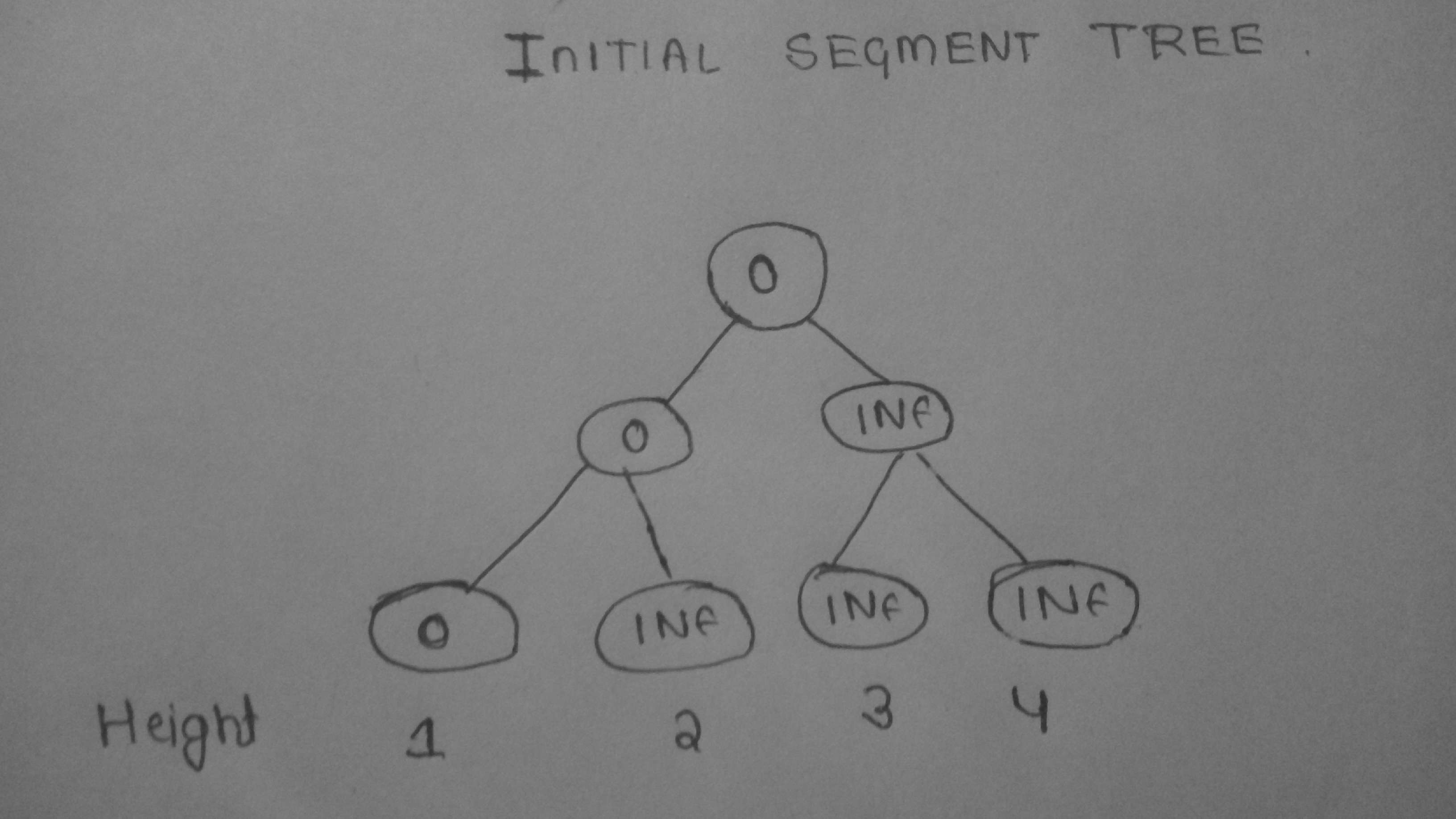
So this will be our segment tree before DFS .
Now , we see for the given tree the longest path between any node and root is of 4 nodes and for computing DP[x] we just need all the DP values of the nodes which lie between x to root i.e for a given height there will be only one DP value . example : for calculating DP[7] , we need DP[1] , DP[2] , DP[4] and DP[1] is at height 1 , DP[2] is at height 2 , DP[4] is at height 3 . So during dfs and updations , at node 7 our segment tree will look like this :
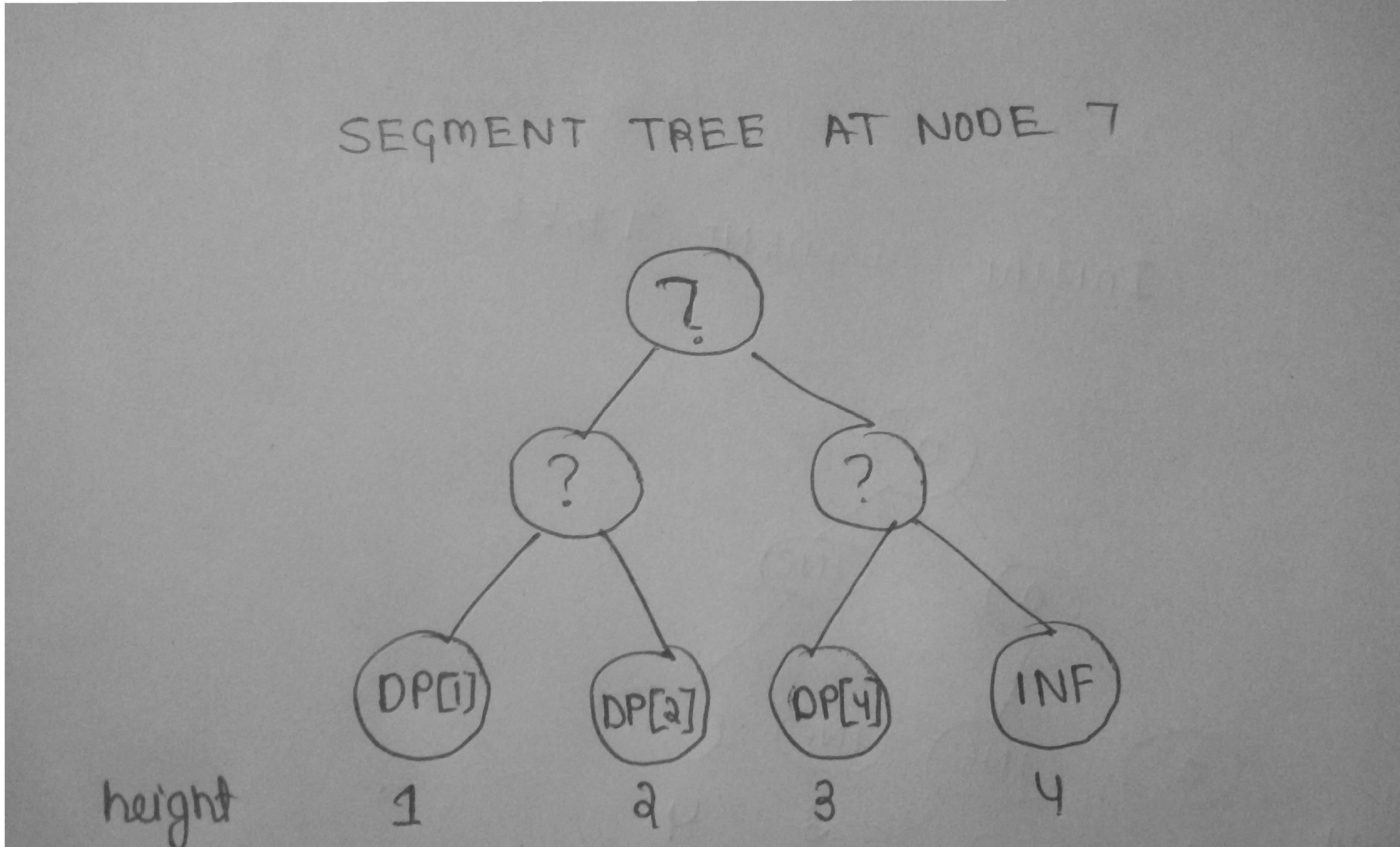
Now at node 7 let there be a ticket with k=2 , w=1 . So now we will query for minimum value between height [2,4] and compute our DP[7] . Now 7 has no children and dfs starts rolling back , and we update height 3 in segment tree with infinity . now at node 5 DPs we require are only DP[1] , DP[2] . The scenario of segment tree will be like this :
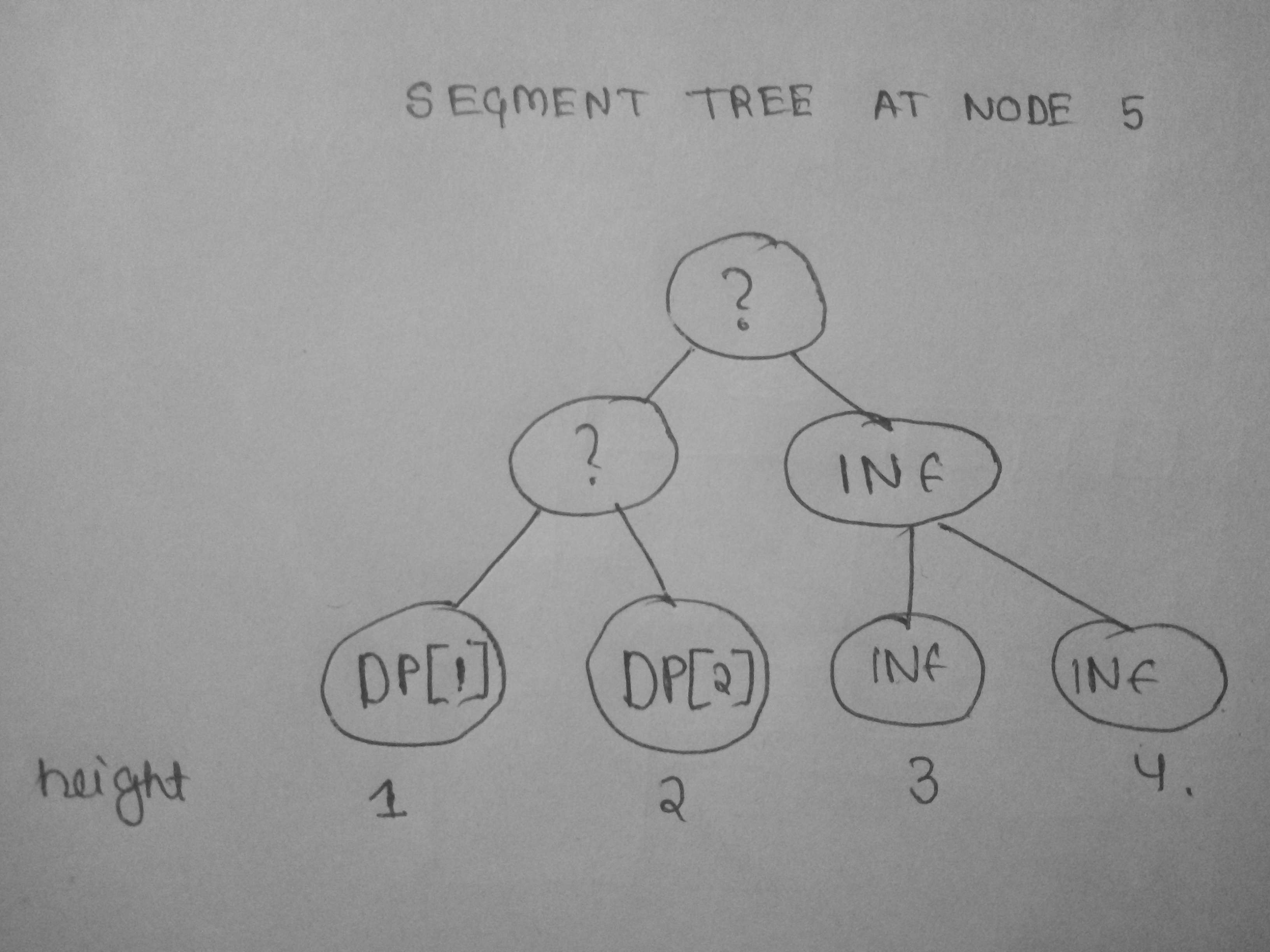
Now Let the ticket available at node 5 be k=3 , w=7 . So now we query over segment tree between [1,3].
