K3TREMAG - Editorial

editorial
, , ,
1

Author: Lakshay
Tester: Divyank
Editorialist: Lakshay

DIFFICULTY:

EASY, MEDIUM.

PREREQUISITES:

Greedy, Math .

EXPLANATION:

image
image613×613 9.45 KB

The first observation is that the edges closer to the source node will contribute more towards the result of Magic function

We can clearly observe that we will remove those C edges from the graph whose contribution i.e., value of (weight) * (distance from leaf) is maximum. So that will help us to greedily select the maximum contributing edge to calculate the minimum answer.

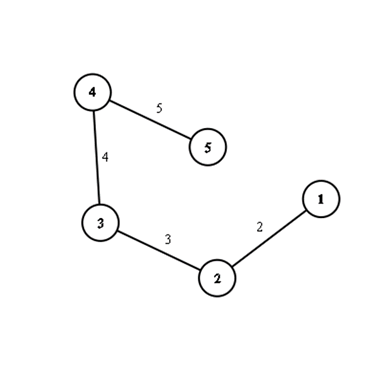
In the sample test case, Source is node 3. If distance[i] denotes the distance of ith node from leaf, then dist = [1,2,5,2,1]

Then we calculate the contribution of each edge in contribution array (order of edges does not matter) then

contribution = [6,2,8,5]

Now we discard the maximum contributing C edges and take the sum of remaining edges and that’s the final answer (we can discard first C elements in the sorted array in decreasing order).

SOLUTIONS:

Setter's Solution 
#include<bits/stdc++.h>
using namespace std;

vector<long long int>dist;
vector<long long int>dp;
vector<vector<pair<long long int,long long int>>>vg;
vector<long long int>vis,vis2;

void dfs1(int node)
{
    vis[node]=1;
    dist[node]=1;

    for(auto x:vg[node])
    {
        if(!vis[x.first])
        {
            dfs1(x.first);
            dist[node]+=dist[x.first];
        }
    }
}

void dfs2(int node)
{
    vis2[node]=1;

    for(auto x:vg[node])
    {
        if(!vis2[x.first])
        {
            long long int val=(long long)x.second*(long long)dist[x.first];
            dp.push_back(val);
             dfs2(x.first);
        }
    }
}

long long solve (int N, int C, int u, vector<vector<int> > edge) {

   vg.resize(N+1);
   vis.resize(N+1,0);
   dist.resize(N+1);
   vis2.resize(N+1,0);
   dp.clear();

    for(int i=1;i<=N;i++)
    {
        vg[i].clear();
        vis[i]=0;
        vis2[i]=0;
        dist[i]=0;
    }

   for(auto x:edge)
   {
       vg[x[0]].push_back({x[1],x[2]});
       vg[x[1]].push_back({x[0],x[2]});
   }

   dfs1(u);

   dfs2(u);

   long long int ans=0;

   sort(dp.rbegin(),dp.rend());

   for(int i=0;i<C;i++)
    dp[i]=0;

    for(int i=0;i<dp.size();i++)
        ans+=dp[i];

    return ans;
}

int main() {

    ios::sync_with_stdio(0);
    cin.tie(0);
    int T;
    cin >> T;
    for(int t_i = 0; t_i < T; t_i++)
    {
        int N;
        cin >> N;
        int C;
        cin >> C;
        int u;
        cin >> u;
        vector<vector<int> > edge(N-1, vector<int>(3));
        for (int i_edge = 0; i_edge < N-1; i_edge++)
        {
            for(int j_edge = 0; j_edge < 3; j_edge++)
            {
                cin >> edge[i_edge][j_edge];
            }
        }

        long long out_;
        out_ = solve(N, C, u, edge);
        cout << out_;
        cout << "\n";
    }
}