PROBLEM LINK:
Author: Dr. M. Kaykobad
Tester: Jingbo Shang
Editorialist: Jingbo Shang
DIFFICULTY:
Medium – Hard
PREREQUISITES:
Greedy
PROBLEM:
Given n files with different sizes, determine the minimum cost of merging files into one file by merging at most m files in a single operation.
EXPLANATION:
Suppose k=3 and n=4 for example. There are two possible plans in the following figure. Obliviously, the left one is much better than the right one since the “lower” floor has more nodes (the cost is only depends on the depth of node).
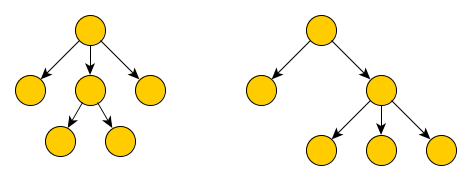
Considering from this view, we can choose the best number of files to merge at the first time by the following procedure:
int k = files.size();
while (k > m) {
k = k / m + k % m;
}
This simulates the procedure of merging k-files as many as possible and getting the final remained files. This remained number is the best choice to merge at the first. After known the best number of files to merge, we definitely choose the smallest k files greedily. Furthermore, we only need O(logN) times to merge into one file (in most steps, k=m). In summary, we can have a greedy algorithm with O(NlogN) if we use fast k-th element algorithm for choose the k smallest.
AUTHOR’S AND TESTER’S SOLUTIONS:
Author’s solution can be found here.
Tester’s solution can be found here.