PROBLEM LINK:
Practice
Contest
Video Editorial
Setter: Vikas Pandey
Tester: Rahul Dugar
Editorialist: Ishmeet Singh Saggu
DIFFICULTY:
Simple
PREREQUISITES:
Basic maths and ad-hoc
PROBLEM:
For a given binary string s of length N and an integer K, where N is divisible by K. Problem asks you to rearrange the characters of the string s to form a lexicographically smallest K- fold string(if it is possible), which can be formed by applying the following operation. We will apply the following operations until the length of the string s becomes K.
- Consider the prefix of length 2*K.
- Check if substring s_1s_2s_3...s_{k-1}s_k is equal to substring s_{2*k}s_{2*k-1}...s_{k+2}s_{k+1}. Note that the order of second substring is reversed. If they are equal, then remove the prefix of length K from string s and continue, otherwise stop(as this arrangement of the string is not K- fold).
Out of all possible K- fold strings output the lexicographically smallest string.
QUICK EXPLANATION:
- Let the total number of continuous segments of length K is numOfSeg = (\frac{N}{K}). Segments of length K are
s_1s_2...s_{k-1}s_k
s_{k+1}s_{k+2}...s_{2*k-1}s_{2*k}
and soon. - Count the total numbers of 0's and 1's in the string s. If the total count of 0's is not divisible by numOfSeg or the total count of 1's is not by divisible numOfSeg the answer will be impossible, else we can make the K- fold string.
- Let the count of 0's in each segment is numZero, and count of 1's in each segment is numOne.
- Construction of the lexicographically smallest string is as follows
- For the first segment i.e. s_1s_2...s_{k-1}s_k, it will be as
000...00111...111where count of 0's will be numZero and count of 1's will be numOne. - For the second segment
111...11000...000. - For the third segment
000...00111...111similar to first segment and so on.
- For the first segment i.e. s_1s_2...s_{k-1}s_k, it will be as
- Concatenate all these segments to get the final answer.
EXPLANATION:
-
For simplicity I will refer substring s_ls_{l+1}...s_{r-1}s_r as [l, r].
-
By applying the operation given in the question you are basically trying to overlap the substring [1, K] in reverse order(i.e. substring s_ks_{k-1}...s_3s_2s_1) onto substring [K+1, 2*K]. Converting string s from [1, N] to [K+1, N].
Let’s first forget about the condition of lexicographically smallest string and analyze the condition to make an K- fold string. So that we can make the necessary rearrangements in the string.
- N should be divisible by K(it is given in the question).
- We will have (\frac{N}{K}) segments of string as [1, K], [K+1, 2*K], … [N-K+1, N]. Let us refer to the quantity (\frac{N}{K}) as numOfSegments
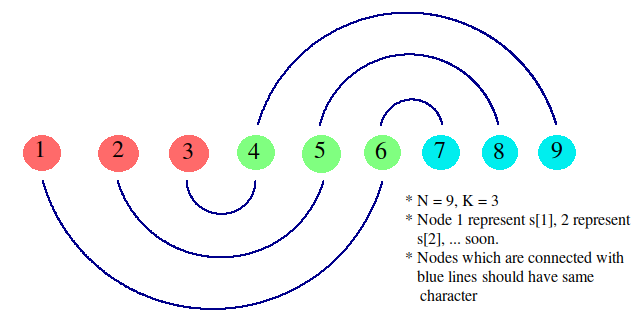
- As to satisfy K- fold condition it is necessary that reverse of substring [1, K] should be equal to substring [K+1, 2*K], the reverse of substring [K+1, 2*K] should be equal to substring [2*K+1, 3*K] and soon. For more clarity about which character is equal to which you can refer to the image below.
- So the above condition implies that count to 0's and 1's in each segment should be equal. So the total count of 0's in string s should be divisible by numOfSegments and the total count of 1's in string s should be divisible by numOfSegments. Otherwise, we won’t be able to equally divide the count of 0's and 1's among (\frac{N}{K}) segments and answer will be
"IMPOSSIBLE".
If the above conditions are satisfied, we can make a K- fold string by rearranging the characters of the string.
Also, one thing to observe here is that if the string s is K- fold, and you fix substring [1, K] then it automatically fixes the substring [K+1, 2*K] which leads to fixing of substring [2*K+1, 3*K] and so on. And why is that? because we are overlapping these substrings over each other.
And this observation will help us to make our K- fold string lexicographically smallest, we just have to construct the substring [1, K] lexicographically smallest and we will get our answer.
Construction :
- Number of 0's in each segment (numZeroes) = \frac{TotalCountOfZeroes}{numOfSegments}
- Number of 1's in each segment (numOnes) = \frac{TotalCountOnes}{numOfSegments}
- The first segment [1, K] will be all 0's (till numZeroes) and then all 1's (till numOnes)
it will look like000...000111...111.
The second segment [K+1, 2*K] will be all 1's (till numOnes) and 0's (till numZeroes)111...111000...000.
The third segment will be all 0's (till numZeroes) and then all 1's (till numOnes)000...000111...111(same as the first segment) and soon. - So basically the odd segments will be like
000...000111...111, and even segment will be like111...111000...000 - And we will concatenate these segments to form the string and hence our answer.
TIME COMPLEXITY:
- We require O(N) operation to count the total number of zeroes and ones and to print the answer. So the total time required per test case is O(N).
- So total time complexity is O(T*N), where T is the number of test cases.
SOLUTIONS:
Setter's Solution
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define pb push_back
#define ff first
#define ss second
#define endl '\n'
void solve()
{
int t;
cin>>t;
assert(1<=t and t<=100);
for(int _=0; _<t; _++)
{
int n, k;
cin>>n>>k;
assert(1<=n and n<=1000);
assert(n%k==0);
string s, ans="";
cin>>s;
assert((int)s.length()==n);
int freq_0=0;
for(auto x:s)
freq_0+=x=='0';
int parts=n/k;
if(freq_0%parts)
{
cout<<"IMPOSSIBLE";
if(_+1<t)
cout<<endl;
continue;
}
int zeros=freq_0/parts, ones=(n-freq_0)/parts;
while(zeros--)
ans+='0';
while(ones--)
ans+='1';
while(parts--)
cout<<ans, reverse(ans.begin(), ans.end());
if(_+1<t)
cout<<endl;
}
}
int32_t main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int t=1;
while(t--)
solve();
return 0;
}
Tester's Solution
#include <bits/stdc++.h>
using namespace std;
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/rope>
using namespace __gnu_pbds;
using namespace __gnu_cxx;
#ifndef rd
#define trace(...)
#define endl '\n'
#endif
#define pb push_back
#define fi first
#define se second
#define int long long
typedef long long ll;
typedef long double f80;
#define double long double
#define pii pair<int,int>
#define pll pair<ll,ll>
#define sz(x) ((long long)x.size())
#define fr(a,b,c) for(int a=b; a<=c; a++)
#define rep(a,b,c) for(int a=b; a<c; a++)
#define trav(a,x) for(auto &a:x)
#define all(con) con.begin(),con.end()
const ll infl=0x3f3f3f3f3f3f3f3fLL;
const int infi=0x3f3f3f3f;
//const int mod=998244353;
const int mod=1000000007;
typedef vector<int> vi;
typedef vector<ll> vl;
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> oset;
auto clk=clock();
mt19937_64 rang(chrono::high_resolution_clock::now().time_since_epoch().count());
int rng(int lim) {
uniform_int_distribution<int> uid(0,lim-1);
return uid(rang);
}
long long readInt(long long l,long long r,char endd){
long long x=0;
int cnt=0;
int fi=-1;
bool is_neg=false;
while(true){
char g=getchar();
if(g=='-'){
assert(fi==-1);
is_neg=true;
continue;
}
if('0'<=g && g<='9'){
x*=10;
x+=g-'0';
if(cnt==0){
fi=g-'0';
}
cnt++;
assert(fi!=0 || cnt==1);
assert(fi!=0 || is_neg==false);
assert(!(cnt>19 || ( cnt==19 && fi>1) ));
} else if(g==endd){
if(is_neg){
x= -x;
}
assert(l<=x && x<=r);
return x;
} else {
assert(false);
}
}
}
string readString(int l,int r,char endd){
string ret="";
int cnt=0;
while(true){
char g=getchar();
assert(g!=-1);
if(g==endd){
break;
}
cnt++;
ret+=g;
}
assert(l<=cnt && cnt<=r);
return ret;
}
long long readIntSp(long long l,long long r){
return readInt(l,r,' ');
}
long long readIntLn(long long l,long long r){
return readInt(l,r,'\n');
}
string readStringLn(int l,int r){
return readString(l,r,'\n');
}
string readStringSp(int l,int r){
return readString(l,r,' ');
}
signed main() {
ios_base::sync_with_stdio(0),cin.tie(0);
srand(chrono::high_resolution_clock::now().time_since_epoch().count());
cout<<fixed<<setprecision(8);
int t=readIntLn(1,100);
while(t--) {
int n=readIntSp(1,1000);
int k=readIntLn(1,n);
assert(n%k==0);
string s=readStringLn(n,n);
int ones=0,zeros=0;
for(char i:s)
if(i=='0')
zeros++;
else
ones++;
if((zeros)%(n/k)==0) {
zeros/=(n/k);
ones/=(n/k);
string ans=string(zeros,'0')+string(ones,'1');
for(int i=0; i<(n/k); i++) {
cout<<ans;
reverse(all(ans));
}
cout<<endl;
} else
cout<<"IMPOSSIBLE"<<endl;
}
assert (getchar() == EOF);
return 0;
}
Editorialist's Solution
#include <bits/stdc++.h>
using namespace std;
void solveTestCase() {
int N, K;
string s;
cin >> N >> K;
cin >> s;
// note, the each segment (1, K), (K+1, 2K) ... (N-K+1, N) with length K should have same number of 0's and 1's.
// there are total N/K segments. And N/K should divide the count of 0's and 1's in order to make a K-fold string.
int zeroCount = 0, oneCount = 0;
for(int i = 0; i < N; i ++) {
if(s[i] == '0') zeroCount ++;
else oneCount ++;
}
int numOfSeg = N/K;
if((zeroCount % numOfSeg) || (oneCount % numOfSeg)) { // so there is no way to divide 0's and 1's in (N/K) segments.
cout << "IMPOSSIBLE\n";
return;
}
// to make lexicographically smallest we will do the following construction.
// {000...00111...111}, {111...11100...000}, ... so on, where each string in {} is one segment of length K, and concatenate them togethor.
zeroCount /= numOfSeg; // getting the count of 0's and 1's in one segment of length K.
oneCount /= numOfSeg;
for(int i = 1; i <= numOfSeg; i ++) { // we will print {000...000111...111} when 'i' is odd and {111...111000...000} when 'i' is even.
if(i % 2) {
for(int j = 1; j <= zeroCount; j ++) {
cout << 0;
}
for(int j = 1; j <= oneCount; j ++) {
cout << 1;
}
}
else {
for(int j = 1; j <= oneCount; j ++) {
cout << 1;
}
for(int j = 1; j <= zeroCount; j ++) {
cout << 0;
}
}
}
cout << '\n';
return;
}
int main() {
ios_base::sync_with_stdio(0); // fast IO
cin.tie(0);
cout.tie(0);
int testCase;
cin >> testCase;
for(int i = 1; i <= testCase; i ++) {
solveTestCase();
}
return 0;
}
Video Editorial
Feel free to share your approach. In case of any doubt or anything is unclear please ask it in the comment section. Any suggestions are welcomed. ![]()

 I tried it many times but I couldn’t figure out this silly mistake
I tried it many times but I couldn’t figure out this silly mistake 