PROBLEM LINK:
Editorialist: Jingbo Shang
DIFFICULTY:
Easy
PREREQUISITES:
sort
PROBLEM:
Given at most K*M intervals [Li, Ri], find the thickest point. That is, for all points x, the most number of intervals covered x.
EXPLANATION:
Let’s split one interval [Li, Ri] into two events, < Li, +1 > and < Ri, -1 >. The first one means the “time” of that event, and the second one means the “delta” of that event. See the following figure for example:
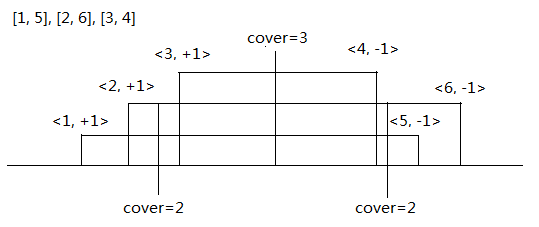
From this idea, we can see that if we order the events in a proper order, the prefix sum can state the cover time. If so, the answer of this problem is just the maximum number among the prefix sum.
But it is ambiguous if we purely ordering the events by “time” when there are two events happened at the same time, such as <1, +1>, <1, -1>. How can we deal with the order between them? In this problem, because the intervals are inclusive and we need to find the maximum covers, we can simply compare these same-“time” events by their "delta"s, in decsending order (i.e <time, +1> is in front of <time, -1>).
All the things remaining is to sort the events by “time” (from early to late) and break the tie using “delta” (from large to small). And then, find the maximum among the prefix sum of “delta”. If we use quick sort here, the time complexity will be O(KMlogKM).