PROBLEM LINK:
Practice
Contest, div. 1
Contest, div. 2
Author: Arun Gupta
Tester: Zhong Ziqian
Editorialist: Oleksandr Kulkov
DIFFICULTY:
EASY-MEDIUM
PREREQUISITES:
DP on substrings
PROBLEM:
Let’s denote reversed string X as X^r. You’re given string S. You have to count number of ways to split it in S=AXBYC such that XY=(XY)^r and neither X nor Y are empty, |S| \leq 10^3.
QUICK EXPLANATION:
Iterate pairs (i,j) to split S=AX|_iBP|_jX^rC. Calculate longest possible |X| over splits with such (i,j) and multiply this value by number of suffix- and prefix-palindromes of the string BP.
EXPLANATION:
Let’s assume that |X| \leq |Y|. Then XY = XPX^r where P = P^r. Let’s iterate through possible positions for AX|BPX^rC split, if we fix such position we may calculate for all possible BP|X^rC splits how long might X^r be. To do this we should calculate longest common prefix of X^rA^r and X^rC. This may be done by quadratic dp (assuming that lcp[0][j] = lcp[i][n+1]=0):
for(int i = 1; i <= n; i++) {
for(int j = i + 1; j <= n; j++) {
lcp[i][j] = (s[i] == s[j]) * (1 + lcp[i - 1][j + 1]);
}
}
Now if we fixed positions i and j of AX|_iBP|_jX^rC splits, we should take the length of longest possible X^r in that position and multiply it with the number of palindromes which start after i and end in j. This also may be done by quadratic dynamic programming. Note that if |X| > |Y| situation is same but we take XY = Y^rPY, thus we should also consider number of prefix-palindromes of string between i and j. It’s all calculated as follows:
for(int i = 1; i <= n; i++) {
is_pal[i][i] = 1;
pre[i][i] = suf[i][i] = 2;
is_pal[i][i - 1] = 1;
pre[i][i - 1] = suf[i][i - 1] = 1;
}
for(int len = 1; len < n; len++) {
for(int i = 1; i + len <= n; i++) {
is_pal[i][i + len] = (s[i] == s[i + len]) * is_pal[i + 1][i + len - 1];
pre[i][i + len] = is_pal[i][i + len] + pre[i][i + len - 1];
suf[i][i + len] = is_pal[i][i + len] + suf[i + 1][i + len];
}
}
Now that we’re done with auxiliary dp’s, we may calculate the final answer. To do this we consider all possible splits AX|_iBP|_jX^rC and add lcp[i][j] \cdot(pre[i+1][j-1]+suf[i+1][j-1]-1) to the answer. We subtracted 1 here because empty string was counted in both pre[i+1][j-1] and suf[i+1][j-1] but it produces same pairs of strings. So, final solution looks like this:
int ans = 0;
for(int i = 1; i <= n; i++) {
for(int j = i + 1; j <= n; j++) {
ans += lcp[i][j] * (pre[i + 1][j - 1] + suf[i + 1][j - 1] - 1);
}
}
AUTHOR’S AND TESTER’S SOLUTIONS:
Author’s solution can be found here.
Tester’s solution can be found here.
Editorialist’s solution can be found here.
3 Likes
Any similar problem for practice ?
11 Likes
Am i the only one who is unable to understand the editorial ? Can someone please provide a simple explanation with small proofs/concepts ?
33 Likes
I imagine there are several different approaches to the problem. I have written my approach here for anyone interested. Below is a copy paste of what I wrote:
Summary
For the Kira Loves Palindromes problem:
Let S be the input string. Define a table D as follows:
D[i,j] = total number of pairs (i,k), (w,j) where i<=k<w<=j such that S[i…k]S[w…j] is a palindrome. Observe that the result is the sum over all D[i,j].
To find the recurrence for D[i,j], define the following three tables, P, LR, RL:
P[i,j] = 1 if S[i…j] is a palindrome and 0 otherwise
LR[i,j] = total number of palindromes S[i…k] where i <= k <= j. In simple words, you want to count how many palindromes start from S[i] and end in some S[k] where i<=k<=j
RL[i,j] = total number of palindromes S[k…j] where i <= k <= j
Then we have that D[i,j] = 1 + D[i+1,j-1] + LR[i+1,j-1] + RL[i+1,j-1] when S[i] = S[j], 0 otherwise.
The recurrences for P, LR and RL are fairly simple (left as an exercise to the reader :P) but you can find my submission here.
12 Likes
Hey , You confused me . LR and RL , are they 2D array as used in final relation for D[ i , j ] ? Or are they 1D array as used to explain what they represent ?
2 Likes
Yes, they are 2D arrays that should help compute D[i,j]. I updated the text because I was using [i][j] and [i,j] to mean the same thing. When I write S[i…j], I mean a substring of S that consists of the characters S[i], S[i+1], …, S[j]. The idea behind LR[i,j] is the following. Let’s say S[i] = S[j] = “a”, then you have a substring in S that looks like “a…a”. Look at a palindrome that starts right after the left most “a”, for example “dbd”, so now your substring looks like “adbd…a”. You can then create a palindrome by combining “abdb” with “a”, i.e. “abdba”. The RL[i,j] (right from left) case covers the palindromes that you can append to the right most occurrence of “a”, for example you could have “a…dcda”, then you can get the palindrome “adcda”.
3 Likes
There is much simpler solution, but no one seem to mention it.
If you observe all the pair of substrings in the solution can be one of the following forms:
WP | Wr (case 1)
W | PWr (case 2)
W | Wr (case 3)
where W is some substring, Wr is its reverse and P is a palindromic substring. Note that | represent where we partition the strings.
Now, if we find all the Palindrome substrings of the given string, it can easily used to find:
- Number of palindrome substrings starting at position s and having length less than equal to l
- Number of palindrome substrings ending at position e and having length less than equal to l
Having pre calculated this, focus on the initial observation. We form our dp such that we choose two substring, first one starting at s and another one ending at e. We can have answer for this selection of s and e only if str[s] == str[e]. if it is the case, we should calculate number of palindrome substrings starting at s+1 and length less than equal to e-s+1 (case 1) and also the number of palindrome substrings ending at e-1 (case 2). Note that you should also add to this dp(s+1, e-1) (case 3).
For answer to the original problem, you must add dp(i,j) for all pairs. You can find this solution on my profile.
10 Likes
@kmampent Can you explain how the matrix P is being populated? I thought of making all the diagonal elements 1 as they will be a palindrome. Then suppose if i and j are the starting and ending indexes of a substring, then we can check if it is a palindrome by dp[i][j] = dp[i+1][j-1] && word[i] == word[j]…but I am still unable to understand how the matrix will be filled with my approach(order of filling)…can you please explain it?
Yes you are correct, the diagonal will be 1. Then I believe the easiest way to populate it is as depicted by the following picture for a table of size 5x5:
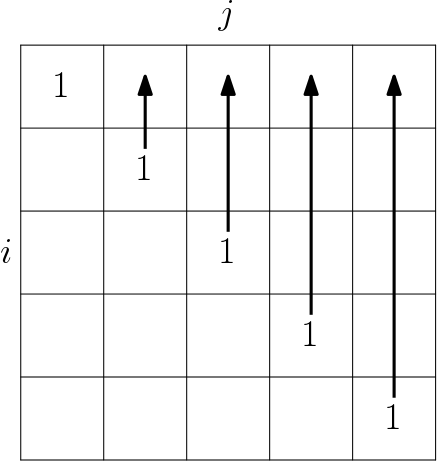
you can then have the following two loops:
for j = 0 to n-1
for i = j to 0
if i == j (diagonal case)
else (any case where i < j)
@kmampent This was the logic I thought of to calculate P
for i = 0 to n:
P[i][i] = 1
for i = 0 to n-1:
P[i][i+1] = s[i] == s[i+1] ? 1 : 0
for i = 0 to n:
for j = 0 to n:
if (abs(i-j) == 1 || i >= j):
continue
P[i][j] = P[i+1][j-1] && s[i] == s[j]
I was not able to check for substrings of length 2 using dp[i][i] as I think that it is necessary to check if both characters are equal or not manually in case of substrings of length 2. So I manually checked for them in my second loop
Will it form the matrix P correctly?
Can I replace your code for computeP() with this code?
Also, I have one more doubt. Why are you filling the columns first rather than rows while computing RL and DP?
Thanks @kmampent and @surprised1 for your approaches  And as @aryanc403 mentioned, other solutions will be appreciated
And as @aryanc403 mentioned, other solutions will be appreciated 
I solved this problem by counting the palindromes starting and ending at every position of the string and sorting them by length. Now, for each pair of positions in the string, I checked the number of characters for which the characters starting from and ending on the positions is same. The result will be for every length, the number of palindromes starting from each position of starting and ending character + 1 (for taking no palindromes). We can preprocess and store palindromes for every pair of positions to get an acceptable solution. Here is link to my solution.
1 Like
@surprised1 Wow simple enough to understand .
It will be helpful if you can give a link to your solution because there is no navigation link to go direct to your profile from discuss.
1 Like
Let me present my solution through an example.
Approach - For each pair of indices 1≤ i < j ≤ n ,find the number of ways of finding string s1 and s2 such that s1 + s2 is a palindrome and s1 start at i and s2 end at j. Then we can just loop over all i and j and sum up to find our answer.
But HOW ?
Lets think inductively ( DP? )
Now consider this example
s = abcdecba
Consider i = 1 & j = 8
a bcdecb a
Now since, s_i == s_j implies it is possible to find such s1 and s2 ( Why? )
Clearly once such possibility is s1 = "a" and s2 = "a"
Next lets check for other ways :
- Case 1 :
s1 = "ab.." and s2 = "..ba". Clearly the number of ways of doing so is equal to number of ways of finding s1 and s2 with i = 2 and j = 7
- Case 2:
s1 = "ab.." and s2 = "a".
Aha! Now we arised with a problem, how many such strings are possible?
Should I loop and find out in O(n^3)?
Lets check what we actually need!
Requirement 1 - Number of Palindromic substrings starting at i + 1 ( Isn’t it? )
- Case 3:
s1 = "a" and s2 = "..ba".
Kinda similar to Case 2!
Same requirement?
Nope! But similar!
Requirement 2 - Number of Palindromic substrings ending at j - 1 ( Similar? )
Now, Our Target is to find these 2 requirements in O(n^2)
Requirement 1
For each pair 1 \le i \le j \le n Find the number of substrings of “s_i{s}_{i+1}......{s}_{j-1}s_j” which start with s_i and is a palindrome! ( Right? )
Similarly for Requirement 2
How?
Hint: Make isPal[i][j] where isPal[i][j] = 1 if “s_i{s}_{i+1}......{s}_{j-1}s_j” is a Palindrome else isPal[i][j] = 0 ( DP? )
Still got Doubt? Ask in comments! 
Link to My Solution KLPM ( KMP? )
20 Likes
I have also used other approach as mentioned by some others in the comments. Link to rather verbose solution- CodeChef: Practical coding for everyone
Damn! This problem has given me nightmares.
2 Likes
@knakul853 yes sure, CodeChef: Practical coding for everyone
I generally keep my solutions clean, so it should be self explanatory. 
The final answer is summation or solvedp(i, j) for all possible values of i, j.
Very detailed and simple explanation
3 Likes
can anyone suggest me more dp questions for practise

 And as
And as