PROBLEM LINK:
Editorialist: Soumik Sarkar
DIFFICULTY:
HARD
PREREQUISITES:
Binary search, Numerical integration
PROBLEM:
Find the radius of a circle such that the average distance from any point inside the circle to a fixed point P located outside the circle at d_{min} distance from the circumference equals D_{avg}.
QUICK EXPLANATION:
The average distance is a monotonously increasing function of the radius. Binary search on the radius to find the value for which average distance is D_{avg}. The average distance can be computed through definite integrals whose limits depend on the radius.
EXPLANATION:
It is clear that D_{avg} is a function of the radius r and d_{min}. Since d_{min} is constant, it solely depends on r. The key observation is that D_{avg} monotonously increases with increase in r. Hence it is possible to use binary search on r to get the answer.
But how do we calculate D_{min} for some r? Surely we cannot find the distance from each of the infinite points inside the circle to P and take their average…
Actually we can, thanks to calculus! If you are not familiar with calculus, and even if you are, I would love to recommend this Essence of calculus playlist by 3Blue1Brown.
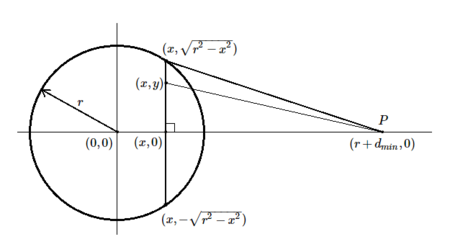
Consider our circle on the X-Y plane with the center at (0, 0) and radius r. The point P is located at (r+d_{min}, 0). Let f(x, y) be the function that returns the distance between the points (x, y) and P. So
Now imagine if for every point in the circle we could compute f(x, y) and plot its value as a point above it in 3D space. Then the entire plot would form a surface above the X-Y plane. Then the required D_{avg} is just the average height of a point on this surface. And this is nothing but the volume under the surface divided by the area it covers on the X-Y plane. The latter is just the area of the circle, so the main task is to find the volume.
For example, for r = 20 and d_{min} = 5, the volume of this structure needs to be calculated.
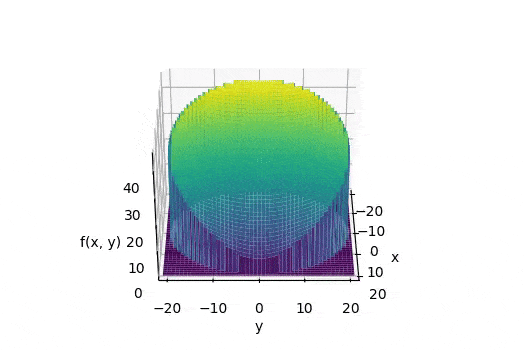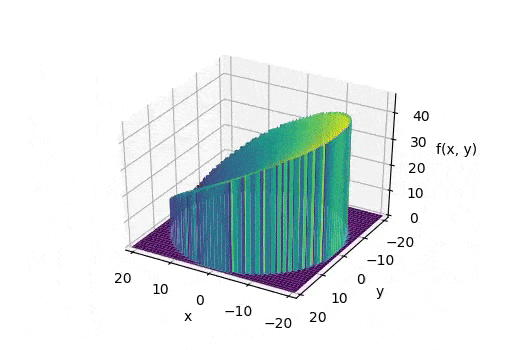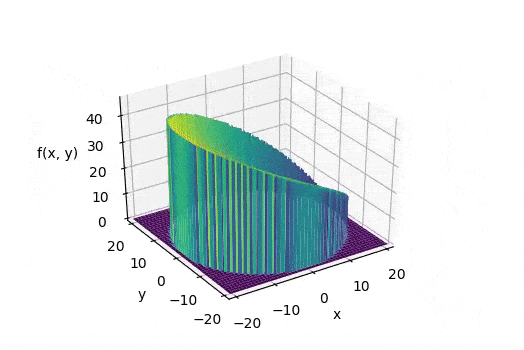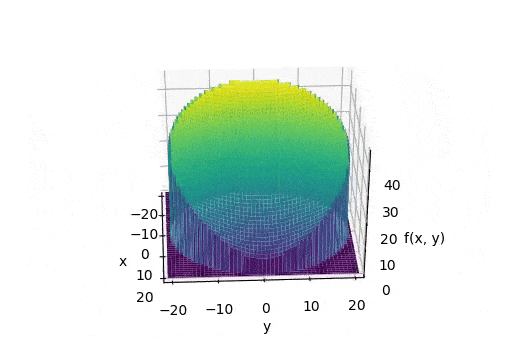
The volume under the surface is the double integral of f over the domain of the circle
This form doesn’t help us, so let us separately integrate over x and y. Inside the circle x ranges from -r to r. And for a particular x, y ranges from -\sqrt{r^2 - x^2} to \sqrt{r^2 - x^2}. Notice that f(x, y) = f(x, -y), so to keep things simple we can find the integral over the upper half of the circle only, and double it to get the total volume. Over the upper half only, y ranges from 0 to \sqrt{r^2 - x^2}.
Let Y = \sqrt{r^2 - x^2} and a = r+d_{min}-x. Then by using standard formulae
We still have an integration left to perform and it looks terrible already. Luckily, being programmers, we can numerically integrate over x. The simplest method is the rectangle method. Better methods such as the trapezoidal rule or Simpson’s 1/3 rule can also be used. A sufficiently small size of the intervals should be chosen for the error to be small. Around 10^4 divisions works fine.
Alternate inner integral (easier)
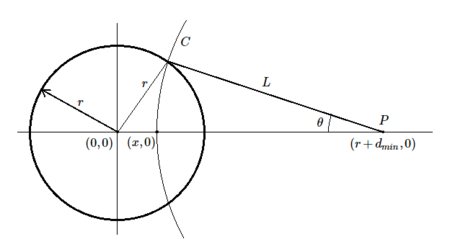
As can be seen, integrating the term \sqrt{(r+d_{min}-x)^2 + y^2} is complicated, but there is a smarter way. Consider a curve C which is a circular arc with center P. Instead of integrating over vertical lines as before, we can instead perform line integrals along curve such as these from the x-axis to the point where it intersects the circumference. Why is this easier? That’s because all points on this curve are at the same distance from P. Let this distance be L, then the line integral is just L times the length of the C.
The angle \theta can be obtained by using the law of cosines.
The length of C is given by L \theta. Then the line integral can be obtained as L^2 \theta. The rest of the algorithm remains the same. The new integral to be calculated is below where L and \theta are determined by x as shown above.
Regardless of the integral used, once the volume V is obtained the average distance to P can be calculated as V / \pi r^2. Hence now it is possible to binary search over r to find the answer.
Each integration uses \approx 10^4 iterations, and there are \log_2(\varepsilon \cdot D_{avg}) integrations performed by the binary search procedure where \varepsilon is the acceptable error. So complexity is \mathcal{O}(10^4 \log(\varepsilon \cdot D_{avg})).
EDITORIALIST’S SOLUTION:
Editorialist’s solution can be found here.